已知函数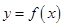 在
在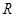 上的图像是连续不断的一条曲线, 在用二分法研究函数
上的图像是连续不断的一条曲线, 在用二分法研究函数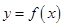 的零点时, 第一次计算得到数据:
的零点时, 第一次计算得到数据: ,根据零点的存在性定理知存在零点
,根据零点的存在性定理知存在零点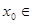 , 第二次计算 , 以上横线处应填的内容为( )
, 第二次计算 , 以上横线处应填的内容为( )
A.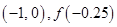 |
B.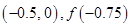 |
C.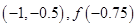 |
D.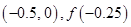 |
关于函数 ,下列说法错误的是( )
,下列说法错误的是( )
A. 是 是 的极小值点 的极小值点 |
B.函数 有且只有1个零点 有且只有1个零点 |
C.存在正实数 ,使得 ,使得 恒成立 恒成立 |
D.对任意两个正实数 ,且 ,且 ,若 ,若 ,则 ,则 |
对于函数 ,如果存在实数
,如果存在实数 、
、 使得
使得 ,那么称
,那么称 为
为 的生成函数.
的生成函数.
(1)下面给出两组函数, 是否为
是否为 的生成函数?并说明理由;
的生成函数?并说明理由;
第一组: ;
;
第二组: .
.
(2)设 ,
, ,
, ,生成函数
,生成函数 ,若不等式
,若不等式 在
在 上有解,求实数t的取值范围.
上有解,求实数t的取值范围.
已知函数f(x)= ,曲线
,曲线 在点(0,2)处的切线与
在点(0,2)处的切线与 轴交点的横坐标为-2.
轴交点的横坐标为-2.
(Ⅰ)求a;
(Ⅱ)当 时,曲线
时,曲线 与直线
与直线 只有一个交点,求x的取值范围.
只有一个交点,求x的取值范围.
已知定义在R上的函数f(x)的图象是连续不断的,且有如下对应值表:
| x |
1 |
2 |
3 |
4 |
| f (x) |
6.1 |
2.9 |
-3.5 |
-5.5 |
那么函数f (x)一定存在零点的区间是 ( )
A.(-∞,1) B.(1,2) C.(2,3) D.(3,+∞)
设函数 .
.
(1)若函数 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
已知函数 若存在实数
若存在实数 ,使函数
,使函数 有两个零点,则实数
有两个零点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. |
B. |
C. |
D. |