山东省济宁市兖州区高一上学期期中考试数学试卷
已知定义在R上的函数f(x)的图象是连续不断的,且有如下对应值表:
| x |
1 |
2 |
3 |
4 |
| f (x) |
6.1 |
2.9 |
-3.5 |
-5.5 |
那么函数f (x)一定存在零点的区间是 ( )
A.(-∞,1) B.(1,2) C.(2,3) D.(3,+∞)
若奇函数 在区间[3,7]上是增函数且最小值为5,则
在区间[3,7]上是增函数且最小值为5,则 在区间
在区间 上是( )
上是( )
A.增函数且最大值为 |
B.增函数且最小值为 |
C.减函数且最小值为 |
D.减函数且最大值为 |
下列说法中,正确的是 ( )
| A.对任意x∈R,都有3x>2x; |
B.y=( )-x是R上的增函数; )-x是R上的增函数; |
C.若x∈R且 ,则 ,则 ; ; |
D.在同一坐标系中,y=2x与 的图象关于直线 的图象关于直线 对称. 对称. |
设函数 的定义域为
的定义域为 ,且
,且 是奇函数,
是奇函数, 是偶函数,则下列结论中正确的( )
是偶函数,则下列结论中正确的( )
A. 是偶函数 是偶函数 |
B. 是奇函数 是奇函数 |
C. 是奇函数 是奇函数 |
D. 是奇函数 是奇函数 |
对于任意实数x,符号 [x]表示不超过x的最大整数(如[-1.5]=-2,[0]=0,[2.3]=2),则 的值为 ( )
的值为 ( )
| A.0 | B.-2 | C.-1 | D.1 |
已知函数f(x)=4x2-kx-8在[5,20]上具有单调性,则实数k的取值范围为_________________.
定义在R上的偶函数f(x)在[0,+∞)上单调递减,且 ,则满足
,则满足 的x的集合为____________________.
的x的集合为____________________.
集合A={x|3≤x<10},B={x|2<x<7},C={x|x<a},
(Ⅰ)求A∪B;
(Ⅱ)求(CRA)∩B;
(Ⅲ)若A∩C≠ ,求a的取值范围.
,求a的取值范围.
已知函数 2≤x≤8.
2≤x≤8.
(Ⅰ)令 ,求y关于t的函数关系式,并写出t的范围;
,求y关于t的函数关系式,并写出t的范围;
(Ⅱ)求该函数的值域.
已知函数 .
.
(Ⅰ)求证:不论a为何实数f(x)在(﹣∞,+∞)上为增函数;
(Ⅱ)若f(x)为奇函数,求a的值;
(Ⅲ)在(Ⅱ)的条件下,求f(x)在区间[1,5)上的最小值.
某校学生研究性学习小组发现,学生上课的注意力指标随着听课时间的变化而变化,老师讲课开始时,学生的兴趣激增;接下来学生的兴趣将保持较理想的状态一段时间,随后学生的注意力开始分散.设f(t)表示学生注意力指标,该小组发现f(t)随时间t(分钟)的变化规律(f(t)越大,表明学生的注意力越集中)如下: (a>0,且a≠1)
(a>0,且a≠1)
若上课后第5分钟时的注意力指标为140,回答下列问题:
(Ⅰ)求a的值;
(Ⅱ)上课后第5分钟时和下课前5分钟时比较,哪个时间注意力更集中?
(Ⅲ)在一节课中,学生的注意力指标至少达到140的时间能保持多长?
 则
则 等于 ( )
等于 ( ) 



 的定义域是 ( )
的定义域是 ( )




 的图象是 ( )
的图象是 ( )
 是定义在
是定义在 上的偶函数,且
上的偶函数,且 ,则下列各式一定成立的是 ( )
,则下列各式一定成立的是 ( )



 ,则
,则 的值是 ( )
的值是 ( )

 图象过点
图象过点 ,则
,则
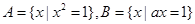 ,若
,若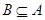 ,则实数
,则实数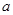 的值为 .
的值为 .
 ,试用
,试用 表示
表示 .
. 是定义在
是定义在 内的增函数,且满足
内的增函数,且满足 .
. ;
; 的解集.
的解集. 粤公网安备 44130202000953号
粤公网安备 44130202000953号