湖南省有许多旅游景点，某同学利用寒暑假旅游了张家界、南岳、韶山、岳阳楼和桃花源等5个景点，并收藏有张家界纪念门票3张，南岳纪念门票2张，韶山、岳阳楼、桃花源纪念门票各1张，现从中随机抽取5张.
（Ⅰ）求抽取的5张门票中恰有3个或恰有4个景点的概率；
（Ⅱ）若抽取的5张门票中5个景点都有记10分，恰有4个景点记8分，恰有3个景点记6分，依此类推.设
表示所得的分数，求的分布列和数学期望.
某研究机构准备举行一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版本教材的教师人数如下表所示：
| 版本 |
人教A版 |
人教B版 |
苏教版 |
北师大版 |
| 人数 |
20 |
15 |
5 |
10 |
（Ⅰ）从这50名教师中随机选出2名，求2人所使用版本相同的概率；
（Ⅱ）若随机选出2名使用人教版的教师发言，设使用人教A版的教师人数为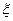
，求随机变量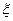的分布列和数学期望。
某城市有甲、乙、丙、丁4个旅游景点，一位客人游览这4个景点的概率都是0.6，且客人是否游览哪个景点互不影响．设
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值．
（1）求的分布列及数学期望；
（2）记“函数
在区间
上单调递增”为事件A，求事件A的概率．
有红蓝两粒质地均匀的正方体骰子，红色骰子有两个面是8，四个面是2，蓝色骰子有三个面是7，三个面是1，两人各取一只骰子分别随机掷一次，所得点数较大者获胜。
（Ⅰ）分别求出两只骰子投掷所得点数的分布列及期望；
（Ⅱ）求投掷蓝色骰子者获胜的概率是多少？
甲，乙两个同学同时报名参加某重点高校
年自主招生，高考前自主招生的程序为审核材料和文化测试，只有审核过关后才能参加文化测试，文化测试合格者即可获得自主招生入选资格.已知甲，乙两人审核过关的概率分别为
，
，审核过关后，甲，乙两人文化测试合格的概率分别为
，
.
(1)求甲，乙两人至少有一人通过审核的概率；
(2) 设
表示甲，乙两人中获得自主招生入选资格的人数，求的数学期望.
如图 A B两点有5条线并联，它们在单位时间内能通过的信息依次为2、3、4、3、2，现从中任取三条线且记在单位时间内通过的信息总量为ζ。
（Ⅰ）写出信息总量ζ的分布布列；
（Ⅱ）求信息总量ζ的数学期望。
（1） 求乙运动员击中8环的概率，并求甲、乙同时击中9环以上（包括9环）的概率。
（2） 求甲运动员射击环数的概率分布列及期望；若从甲、乙运动员中只能挑选一名参加某大型比赛，你认为让谁参加比较合适？
某大学开设甲、乙、丙三门选修课，学生是否选修哪门课互不影响.已知某学生选修甲而不选修乙和丙的概率为0.08，选修甲和乙而不选修丙的概率是0.12，至少选修一门课的概率是0.88，用
表示该学生选修的课程门数和没有 选修的课程门数的乘积.
（1）记“函数f（x）=x2+·x为R上的偶函数”为事件A，求事件A的概率；
（2）求的概率分布和数学期望.
一个袋中装有若干个大小相同的黑球、白球和红球.已知从袋中任意摸出1个球，得到黑球的概率是
；从袋中任意摸出2个球，至少得到1个白球的概率是
.若袋中共有10个球,
（1）求白球的个数；
（2）从袋中任意摸出3个球，记得到白球的个数为
，求随机变量的数学期望E().
设在12个同类型的零件中有2个次品，抽取3次进行检验，每次抽取一个，并且取出不再放回，若以ξ和
分别表示取出次品和正品的个数.
（1）求
的概率分布、期望值及方差；
（2）求的概率分布、期望值及方差.
某地区的一个季节下雨天的概率是0.3，气象台预报天气的准确率为0.8.某厂生产的产品当天怕雨，若下雨而不做处理，每天会损失3 000元，若对当天产品作防雨处理，可使产品不受损失，费用是每天500元.
（1）若该厂任其自然不作防雨处理，写出每天损失
的概率分布，并求其平均值；
（2）若该厂完全按气象预报作防雨处理，以
表示每天的损失，写出的概率分布.
计算的平均值，并说明按气象预报作防雨处理是否是正确的选择？
有甲、乙两个建材厂，都想投标参加某重点建设项目，为了对重点建设项目负责，政府到两建材厂抽样检查，他们从中各取等量的样品检查它们的抗拉强度指数如下：
 |
110 |
120 |
125 |
130 |
135 |
| P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
 |
100 |
115 |
125 |
130 |
145 |
| P |
0.1 |
0.2 |
0.4 |
0.1 |
0.2 |
其中和分别表示甲、乙两厂材料的抗拉强度，在使用时要求抗拉强度不低于120的条件下，比较甲、乙两厂材料哪一种稳定性较好.
粤公网安备 44130202000953号
的分布列及数学期望E
的数学期望