为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前3个小组的频率之比为1：2：3，其中第2小组的频数为12．
（1）求该校报考飞行员的总人数；
（2）以这所学校的样本数据来估计全省的总体数据，若从全省报考飞行员的同学中（人数很多）任选三人，设
表示体重超过60公斤的学生人数，求的分布列和数学期望．
(本题14分)张老师居住在某城镇的A处，准备开车到学校B处上班。若该地各路段发生堵车事件都是独立的，且在同一路段发生堵车事件最多只有一次，发生堵车事件的概率如图。（例如：A→C→D算作两个路段：路段AC发生堵车事件的概率为
，路段CD发生堵车事件的概率为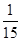
）。（1）请你为其选择一条由A到B的路线，使得途中发生堵车事件的概率最小；（2）若记路线A→C→F→B中遇到堵车次数为随机变量
，求的数学期望
。
（本小题满分12分）某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为
,m,n（m>n）,设该同学三门课程都取得优秀成绩的概率为
,都未取得优秀成绩的概率为
,且不同课程是否取得优秀成绩相互独立．
（1）求m,n；
（2）设X为该同学取得优秀成绩的课程门数,求EX．
（本小题满分12分）在一个盒子中，放有大小相同的红、白、黄三个小球，现从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中，有放回地先后摸出两球，所得分数分别记为
、
，设
为坐标原点，点
的坐标为
，记
．
（I）求随机变量
的最大值，并求事件“取得最大值”的概率；
（2）求随机变量的分布列和数学期望．
（本小题满分12分）一个盒子中装有大量形状大小一样但重量不尽相同的小球，从中随机抽取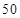
个作为样本，称出它们的重量（单位：克），重量分组区间为
，
，
，
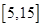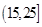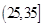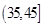，由此得到样本的重量频率分布直方图（如图），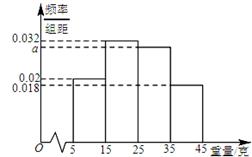
（Ⅰ）求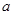
的值，并根据样本数据，试估计盒子中小球重量的众数与平均值；
（Ⅱ）从盒子中随机抽取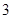
个小球，其中重量在
内的小球个数为
，求的分布列和数学期望. (以直方图中的频率作为概率).
（本小题满分12分）从某小区抽取100户居民进行月用电量调查，发现其用电量都在50度至350度之间，频率分布直方图如图所示．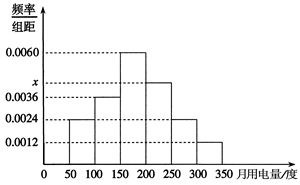
（1）根据直方图求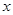
的值，并估计该小区100户居民的月均用电量（同一组中的数据用该组区间的中点值作代表）；
（2）从该小区已抽取的100户居民中，随机抽取月用电量超过250度的3户，参加节约用电知识普及讲座，其中恰有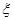
户月用电量超过300度，求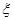的分布列及期望.
（本小题满分10分）袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为
。现有甲、乙两人从袋中轮流、不放回地摸取1球，甲先取，乙后取，然后甲再取……直到袋中的球取完即终止。若摸出白球，则记2分，若摸出黑球，则记1分。每个球在每一次被取出的机会是等可能的。用x表示甲，乙最终得分差的绝对值．
(1)求袋中原有白球的个数；
(2)求随机变量x的概率分布列及期望Ex．
（本小题满分12分）某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为
，得到乙公司和丙公司面试的概率均为p，，且三个公司是否让其面试是相互独立的．记
为该毕业生得到面试的公司个数，若P（＝0）＝
．
（1）求p的值：
（2）求随机变量的分布列及数学期望．
某班同学利用五一节进行社会实践，对[25，55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查，若生活习惯符合低碳观念，则称为“低碳族”，否则称为“非低碳族”，得到如下统计表和各年龄段人数频率分布直方图：
| 组数 |
分组 |
低碳族 的人数 |
占本组 的频率 |
| 1 |
[25，30） |
120 |
0.6 |
| 2 |
[30，35） |
195 |
P |
| 3 |
[35，40） |
100 |
0.5 |
| 4 |
[40，45） |
a |
0.4 |
| 5 |
[45，50） |
30 |
0.3 |
| 6 |
[50，55） |
15 |
0.3 |
（1）请补全频率分布直方图，并求n、a、p的值；
（2）在所得样本中，从[40，50）岁年龄段的“低碳族”中采用分层抽样法抽取18人参加户外低碳体验活动，其中选取3人作为领队，记选取的3名领队中年龄在[40，45）岁的人数为X，求X的分布列和数学期望EX．
某鱼类养殖户在一个鱼池中养殖一种鱼，每季养殖成本为
元，此鱼的市场价格与鱼池的产量均具有随机性，且互不影响，其具体情况如下表：
鱼池产量（ ） |
 |
 |
|
鱼的市场价格（元/） |
 |
 |
| 概率 |
 |
|
|
概率 |
 |
 |
（1）设
表示在这个鱼池养殖
季这种鱼的利润，求的分布列和期望；
（2）若在这个鱼池中连续
季养殖这种鱼，求这季中至少有
季的利润不少于
元的概率．
甲、乙两名篮球运动员，各自的投篮命中率分别为
与
，如果每人投篮两次．
（Ⅰ）求甲比乙少投进一次的概率；
（Ⅱ）若投进一个球得
分，未投进得
分，求两人得分之和
的分布列及数学期望
．
（本小题满分12分）甲、乙两袋中各装有大小相同的小球
个，其中甲袋中红色、黑色、白色小球的个数分别为
、
、
，乙袋中红色、黑色、白色小球的个数均为，某人用左右手分别从甲、乙两袋中取球．
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若左右手依次各取两球，称同一手中两球颜色相同的取法为成功取法，记两次取球的成功取法次数为随机变量
，求的分布列和数学期望．
（本小题满分12分）甲、乙、丙三人射击同一目标，各射击一次，已知甲击中目标的概率为
，乙与丙击中目标的概率分别为
，每人是否击中目标是相互独立的．记目标被击中的次数为
，且的分布列如下表：
（Ⅰ）求的值；
（Ⅱ）求的数学期望．
某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照
的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在
的数据）．
（Ⅰ）求样本容量n和频率分布直方图中x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设
表示所抽取的3名同学中得分在
的学生个数，求的分布列及其数学期望．
粤公网安备 44130202000953号
的社长是高中学生，
的社长是初中学生，高中社长中有
是高一学生，初中社长中有
是初二学生．
，求
．