(本小题满分12分)西安市某中学在每年的11月份都会举行“文化艺术节”,开幕式当天组织举行大型的文艺表演,同时邀请36名不同社团的社长进行才艺展示.其中有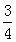 的社长是高中学生,
的社长是高中学生,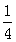 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有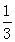 是高一学生,初中社长中有
是高一学生,初中社长中有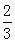 是初二学生.
是初二学生.
(Ⅰ)若校园电视台记者随机采访3位社长,求恰有1人是高一学生且至少有1人是初中学生的概率;
(Ⅱ)若校园电视台记者随机采访3位初中学生社长,设初二学生人数为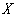 ,求
,求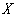 的分布列及数学期望
的分布列及数学期望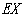 .
.
相关知识点
推荐套卷
 +n-4.
+n-4.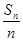 =3n-2.
=3n-2. ,Tn是数列{bn}的前n项和,求使得Tn<
,Tn是数列{bn}的前n项和,求使得Tn<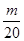 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.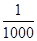 ?
? 粤公网安备 44130202000953号
粤公网安备 44130202000953号