某鱼类养殖户在一个鱼池中养殖一种鱼,每季养殖成本为 元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
元,此鱼的市场价格与鱼池的产量均具有随机性,且互不影响,其具体情况如下表:
鱼池产量( ) ) |
 |
 |
|
鱼的市场价格(元/ ) ) |
 |
 |
| 概率 |
 |
 |
|
概率 |
 |
 |
(1)设 表示在这个鱼池养殖
表示在这个鱼池养殖 季这种鱼的利润,求
季这种鱼的利润,求 的分布列和期望;
的分布列和期望;
(2)若在这个鱼池中连续 季养殖这种鱼,求这
季养殖这种鱼,求这 季中至少有
季中至少有 季的利润不少于
季的利润不少于 元的概率.
元的概率.
相关知识点
推荐套卷
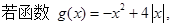
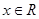 ;
;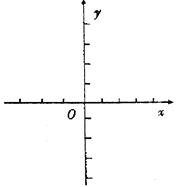
 并
并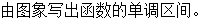
 的定义域为集合
的定义域为集合 ,且
,且 ,
, ;
; ;
; ,求实数
,求实数 的取值范围。
的取值范围。 ;
;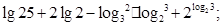
 :
: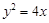 ,过焦点
,过焦点 斜率大于零的直线
斜率大于零的直线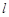 交抛物线于
交抛物线于 、
、 两点,且与其准线交于点
两点,且与其准线交于点 .
.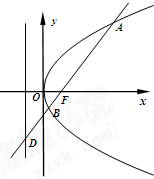
 的长为
的长为 ,求直线
,求直线 ,使得对任意直线
,使得对任意直线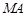 ,
, ,
,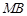 的斜率始终成等差数列,若存在求点
的斜率始终成等差数列,若存在求点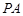 ⊥平面
⊥平面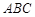 ,
, ,
,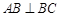 ,
,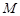 为
为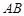 中点.
中点.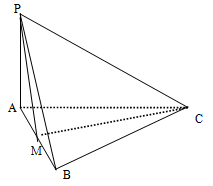
 ;
; 与平面
与平面 所成角的正切值为
所成角的正切值为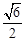 ,求二面角
,求二面角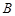 -
- 粤公网安备 44130202000953号
粤公网安备 44130202000953号