（本小题10分）如图，已知抛物线
：
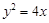，过焦点
斜率大于零的直线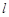
交抛物线于
、
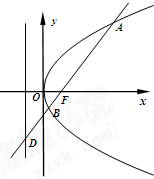
两点，且与其准线交于点
．
（Ⅰ）若线段
的长为
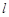，求直线的方程；
（Ⅱ）在上是否存在点
，使得对任意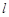直线，直线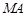
，
，
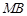的斜率始终成等差数列，若存在求点的坐标；若不存在，请说明理由.
满足
，
，求
的值
是边长为
的正方形
内或边上一动点，
是
中点，求
最大值
的速度向该容器注水，当水深
时，求水面上升的速度
，
，
，
,求数列
，
通项公式
中，三边为
，且
，
，求△相关知识点
推荐套卷
（本小题10分）如图，已知抛物线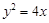：，过焦点斜率大于零的直线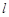交抛物线于、两点，且与其准线交于点．
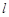（Ⅰ）若线段的长为，求直线的方程；
（Ⅱ）在上是否存在点，使得对任意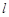直线，直线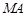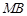，，的斜率始终成等差数列，若存在求点的坐标；若不存在，请说明理由.
粤公网安备 44130202000953号