(本小题满分12分)
已知点列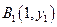 、
、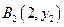 、…、
、…、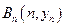 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数 图像上的点,点列
图像上的点,点列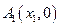 、
、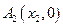 、…、
、…、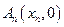 (n∈N)顺次为x轴正半轴上的点,其中
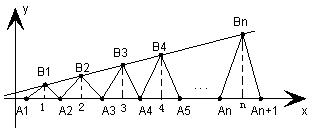
(n∈N)顺次为x轴正半轴上的点,其中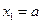 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点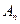 、
、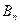 、
、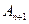 构成一个顶角的顶点为
构成一个顶角的顶点为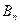 的等腰三角形。
的等腰三角形。
(1)数列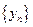 的通项公式,并证明
的通项公式,并证明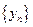 是等差数列;
是等差数列;
(2)证明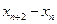 为常数,并求出数列
为常数,并求出数列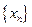 的通项公式;
的通项公式;
(3)上述等腰三角形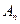
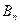
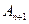 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
推荐套卷
(本小题满分12分)
已知点列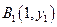 、
、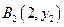 、…、
、…、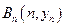 (n∈N)顺次为一次函数
(n∈N)顺次为一次函数 图像上的点,点列
图像上的点,点列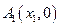 、
、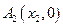 、…、
、…、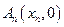 (n∈N)顺次为x轴正半轴上的点,其中
(n∈N)顺次为x轴正半轴上的点,其中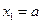 (0<a<1),对于任意n∈N,点
(0<a<1),对于任意n∈N,点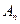 、
、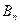 、
、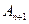 构成一个顶角的顶点为
构成一个顶角的顶点为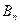 的等腰三角形。
的等腰三角形。

(1)数列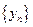 的通项公式,并证明
的通项公式,并证明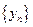 是等差数列;
是等差数列;
(2)证明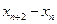 为常数,并求出数列
为常数,并求出数列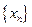 的通项公式;
的通项公式;
(3)上述等腰三角形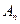
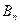
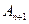 中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。
中,是否存在直角三角形?若有,求出此时a值;若不存在,请说明理由。