（本小题满分12分）某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为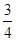
，得到乙公司和丙公司面试的概率均为p，，且三个公司是否让其面试是相互独立的．记
为该毕业生得到面试的公司个数，若P（＝0）＝
．
（1）求p的值：
（2）求随机变量的分布列及数学期望．
相关试题
)=
;
，求f(
终边上的点P与A（a，2a）关于x轴对称（a≠0），角
终边上的点Q与A关于直线y=x对称，求sin
为第三象限角，试判断
的符号.
的终边在y轴上，求sin相关知识点
推荐套卷
（本小题满分12分）某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为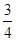，得到乙公司和丙公司面试的概率均为p，，且三个公司是否让其面试是相互独立的．记为该毕业生得到面试的公司个数，若P（＝0）＝．
（1）求p的值：
（2）求随机变量的分布列及数学期望．
粤公网安备 44130202000953号