某区要进行中学生篮球对抗赛，为争夺最后一个小组赛名额，甲、乙、丙三支篮球队要进行比赛，根据规则：每两支队伍之间都要比赛一场；每场比赛胜者得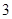
分，负者得
分，没有平局，获得第一名的将夺得这个参赛名额．已知乙队胜丙队的概率为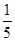
，甲队获得第一名的概率为
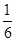，乙队获得第一名的概率为
．
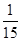（Ⅰ）求甲队分别战胜乙队和丙队的概率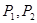
；
（Ⅱ）设在该次比赛中，甲队得分为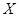
，求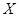的分布列及期望．
（本小题满分14分）如图，
两点之间有5条网线并联，它们能通过的信息量分别为2、3、3、4、4．现从中随机任取2条网线．
（1）设选取的2条网线由
到
通过的信息总量为
，当
时，则保证信息畅通．求线路信息畅通的概率；
（2）求选取的2条网线可通过信息总量的数学期望．
某中学举行了一次“环保知识竞赛”活动．为了了解本次竞赛学生成绩情况，从中抽取了部分学生的分数（得分取正整数，满分为100分）作为样本（样本容量为n）进行统计．按照
的分组作出频率分布直方图，并作出样本分数的茎叶图（图中仅列出了得分在
的数据）．
（Ⅰ）求样本容量n和频率分布直方图中x、y的值；
（Ⅱ）在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取3名同学到市政广场参加环保知识宣传的志愿者活动，设
表示所抽取的3名同学中得分在
的学生个数，求的分布列及其数学期望．
甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2、3、4，乙袋中红色、黑色、白色小球的个数均为3，某人用左手从甲袋中取球，用右手从乙袋中取球，
（1）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（2）若一次在同一袋中取出两球，如果两球颜色相同则称这次取球获得成功。某人第一次左手先取两球，第二次右手再取两球，记两次取球的获得成功的次数为随机变量X，求X的分布列和数学期望．
某公司为招聘新员工设计了一个面试方案:应聘者从
道备选题中一次性随机抽取
道题，按照题目要求独立完成规定:至少正确完成其中
道题的便可通过.已知道备选题中应聘者甲有
道题能正确完成，道题不能完成；应聘者乙每题正确完成的概率都是
，且每题正确完成与否互不影响
（1)分别求甲、乙两人正确完成面试题数的分布列，并计算其数学期望；
（2）请分析比较甲、乙两人谁的面试通过的可能性大？
（本小题满分12分）甲乙两班进行消防安全知识竞赛，每班出
人组成甲乙两支代表队，首轮比赛每人一道必答题，答对则为本队得
分，答错不答都得
分，已知甲队人每人答对的概率分别为
，乙队每人答对的概率都是
．设每人回答正确与否相互之间没有影响，用
表示甲队总得分．
（Ⅰ）求随机变量的分布列及其数学期望
;
（Ⅱ）求在甲队和乙队得分之和为
的条件下，甲队比乙队得分高的概率．
从某批产品中，有放回地抽取产品两次，每次随机抽取1件，假设事件
：“取出的2件产品中至多有1件是二等品”的概率
．
（Ⅰ）求从该批产品中任取1件是二等品的概率
；
（Ⅱ）若该批产品共20件，从中任意抽取2件，X表示取出的2件产品中二等品的件数，求X的分布列与期望．
（本小题满分12分）根据以往的经验，某工程施工期间的降水量X（单位：mm）对工期的影响如下表：
| 降水量X |
X<300 |
300≤X<700 |
700≤X<900 |
X≥900 |
| 工期延 |
|
|
|
|
| 误天数Y |
0 |
2 |
6 |
10 |
历年气象资料表明，该工程施工期间降水量X小于300,700,900的概率分别为0．3 ,0．7 ,0．9．求：
（Ⅰ）工期延误天数Y的均值与方差；
（Ⅱ）在降水量X至少是300的条件下，工期延误不超过6天的概率．
某校高一年级开设
，
，
，
，
五门选修课，每位同学须彼此独立地选三门课程，其中甲同学必选课程，不选课程，另从其余课程中随机任选两门课程．乙、丙两名同学从五门课程中随机任选三门课程．
（Ⅰ）求甲同学选中课程且乙同学未选中课程的概率；
（Ⅱ）用
表示甲、乙、丙选中课程的人数之和，求的分布列和数学期望．
（本小题满分16分）袋中有大小相同的三个球，编号分别为1,2,3．从袋中每次取出一个球，若取到的球的编号为2，则把该球编号记下再把编号数改为1后放回袋中继续取球；若取到球的编号为奇数，则取球停止，取球停止后用X表示“所有被取球的编号之和”。
（1）求X的概率分布；
（2）求X的数学期望及方差．
在抽样方法中，有放回抽样与无放回抽样中个体被抽到的概率是不同的，但当总体的容量很大而抽取的样本容量很小时，无放回抽样可以近似看作有放回抽样。现有一大批产品，采用随机抽样的方法一件一件抽取进行检验。若抽查的4件产品中未发现不合格产品，则停止检查，并认为该批产品合格；若在查到第4件或在此之前发现不合格产品，则也停止检查，并认为该批产品不合格。假定该批产品的不合格率为0．1，设检查产品的件数为X。
（Ⅰ）求随机变量X的分布列和数学期望；
（Ⅱ）通过上述随机抽样的方法进行质量检查，求认为该批产品不合格的概率
（本小题满分12分）某同学参加语、数、外三门课程的考试,设该同学语、数、外取得优秀成绩的概率分别为
,m,n（m>n）,设该同学三门课程都取得优秀成绩的概率为
,都未取得优秀成绩的概率为
,且不同课程是否取得优秀成绩相互独立．
（1）求m,n；
（2）设X为该同学取得优秀成绩的课程门数,求EX．
（本小题满分12分） 甲、乙两人轮流投篮,每人每次投一球,．约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束．设甲每次投篮投中的概率为
,乙每次投篮投中的概率为
,且各次投篮互不影响．
（Ⅰ） 求甲获胜的概率;
（Ⅱ） 求投篮结束时甲的投篮次数
的分布列与期望
（本小题满分10分）袋中装有黑球和白球共7个，从中任取2个球都是白球的概率为
。现有甲、乙两人从袋中轮流、不放回地摸取1球，甲先取，乙后取，然后甲再取……直到袋中的球取完即终止。若摸出白球，则记2分，若摸出黑球，则记1分。每个球在每一次被取出的机会是等可能的。用x表示甲，乙最终得分差的绝对值．
(1)求袋中原有白球的个数；
(2)求随机变量x的概率分布列及期望Ex．
粤公网安备 44130202000953号
