高中数学随机思想的发展试题

（本小题满分12分）现有4名学生参加演讲比赛，有A、B两个题目可供选择．组委会决定让选手通过掷一枚质地均匀的骰子选择演讲的题目，规则如下：选手掷出能被3整除的数则选择A题目，掷出其他的数则选择B题目．
（1）求这4个人中恰好有1个人选择B题目的概率；
（2）用X、Y分别表示这4个人中选择A、B题目的人数，记，求随机变量的分布列与数学期望．

（本小题满分14分）某中学在高二开设了A，B，C，D共4门选修课，每个学生必须且只需选修1门选修课，对于该年级的甲、乙、丙3名学生。
（Ⅰ）求这3名学生选择的选修课互不相同的概率；
（Ⅱ）求恰有2门选修课没有被这3名学生选择的概率；
（Ⅲ）求A选修课被这3名学生选择的人数的数学期望．

（本小题共13分）某商场一号电梯从1层出发后可以在2、3、4层停靠．已知该电梯在1层载有4位乘客，假设每位乘客在2、3、4层下电梯是等可能的．
（Ⅰ） 求这4位乘客中至少有一名乘客在第2层下电梯的概率；
（Ⅱ） 用表示4名乘客在第4层下电梯的人数，求的分布列和数学期望．

（本小题满分14分）某商场进行促销活动，到商场购物消费满100元就可转动转盘（转盘为十二等分的圆盘）一次进行抽奖，满200元转两次，以此类推（奖金累加）；转盘的指针落在A区域中一等奖，奖10元，落在B、C区域中二等奖，奖5元，落在其它区域则不中奖．一位顾客一次购物消费268元，

（Ⅰ）求该顾客中一等奖的概率；
（Ⅱ）记为该顾客所得的奖金数，求其分布列；
（Ⅲ）求数学期望（精确到0.01）．

（本小题满分13分）为了参加广州亚运会，从四支较强的排球队中选出18人组成女子排球国家队，队员来源人数如下表：

队别	北京	上海	天津	八一
人数	4	6	3	5

 
（Ⅰ）从这18名队员中随机选出两名，求两人来自同一支队的概率；
（Ⅱ）中国女排奋力拼搏，战胜韩国队获得冠军．若要求选出两位队员代表发言，设其中来自北京队
的人数为，求随机变量的分布列，及数学期望．

（本小题共13分）甲、乙、丙三人参加了一家公司的招聘面试，面试合格者可正式签约，甲表示只要面试合格就签约．乙、丙则约定：两人面试都合格就一同签约，否则两人都不签约．设甲面试合格的概率为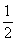，乙、丙面试合格的概率都是，且面试是否合格互不影响．
（Ⅰ）求至少有1人面试合格的概率；
（Ⅱ）求签约人数的分布列和数学期望

（本小题满分13分）在某校教师趣味投篮比赛中,比赛规则是: 每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖．已知教师甲投进每个球的概率都是．
（Ⅰ）记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；
（Ⅱ）求教师甲在一场比赛中获奖的概率；
（Ⅲ）已知教师乙在某场比赛中，6个球中恰好投进了4个球，求教师乙在这场比赛中获奖的概率；教师乙在这场比赛中获奖的概率与教师甲在一场比赛中获奖的概率相等吗？

（本小题满分12分） 学生的学习能力参数可有效衡量学生的综合能力，越大，综合能力越强，为推动数学知识的发展，提高学生的综合能力。某校根据学生的学习能力参数将参加数学竞赛小组的学生分成了如下三类：

学习能力参数	学习能力参数
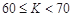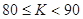学生人数（人）	15	10

 
某研究性学习小组，从该竞赛小组中按分层抽样的方法随机选取了人，根据其学习能力参数，作出了频率与频数的统计表：

分组	频数（人）	频率
	3
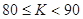合计

 
（1）求，，，的值
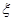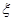（2）规定：学习能力参数不少于70称为优秀。若从这人中任选人，记抽到到的优秀人数为随机变量，求的分布列和数学期望

（本小题满分1 2分）2014年我国公布了新的高考改革方案，在招生录取制度改革方面，普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制，普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩。
为了解公众对“改革方案”的态度，随机抽查了50人，将调查情况进行整理后制成下表：

（1）完成被调查人员的频率分布直方图；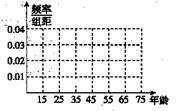

（2）若年龄在[15，25），[55，65）的被调查者中赞成人数分别为4人和3人，现从这两组的被调查者中各随机选取两人进行追踪调查，记选中的4人中不赞成“改革方案”的人数为X，求随机变量X的分布列和数学期望．

（本小题满分12分）甲、乙两袋中各装有大小相同的小球9个，其中甲袋中红色、黑色、白色小球的个数分别为2，3，4，乙袋中红色、黑色、白色小球的个数均为3，某人用左右手分别从甲、乙两袋中取球．
（Ⅰ）若左右手各取一球，求两只手中所取的球颜色不同的概率；
（Ⅱ）若左右手依次各取两球，称同一手中 两球颜色相同的取法为成功取法，记两次取球（左右手依次各取两球为两次取球）的成功取法次数为随机变量X，求X的分布列和数学期望．

（本小题满分12分）某军区新兵步枪射击个人平均成绩（单位：环）服从正态分布，从这些个人平均成绩中随机抽取个，得到如下频数分布表：

频数

（Ⅰ）求和的值（用样本数学期望、方差代替总体数学期望、方差）；
（Ⅱ）如果这个军区有新兵名，试估计这个军区新兵步枪射击个人平均成绩在区间上的人数
[参考数据：，若，则，，]．

为了促进学生的全面发展，某市教育局要求本市所有学校重视社团文化建设，2014年该市某中学的某新生想通过考核选拨进入该校的“电影社”和“心理社”，已知该同学通过考核选拨进入这两个社团成功与否相互独立．根据报名情况和他本人的才艺能力，两个社团都能进入的概率为，至少进入一个社团的概率为，并且进入“电影社”的概率小于进入“心理社”的概率．
（Ⅰ）求该同学分别通过选拨进入“电影社”的概率和进入“心理社”的概率；
（Ⅱ）学校根据这两个社团的活动安排情况，对进入“电影社”的同学增加1个校本选修课学分，对进入“心理社”的同学增加0．5个校本选修课学分．求该同学在社团方面获得校本选修课学分分数的分布列和数学期望．

某校举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本．对高一年级的100名学生的成绩进行统计，得到成绩分布的频率分布直方图如图：

（1）若规定60分以上（包括60分）为合格，计算高一年级这次知识竞赛的合格率；
（2）将上述调查所得到的频率视为概率.现在从该校大量高一学生中，采用随机抽样方法每次抽取1名学生，抽取3次，记被抽取的3名学生中的合格人数为.若每次抽取的结果是相互独立的，求的分布列和期望；

	高一	高二	合计
合格人数
不合格人数
合计

 
（3）若高二年级这次知识竞赛的合格率为60%，由以上统计数据填写2×2列联表，并问是否有99%的把握认为“这次知识竞赛的成绩与年级有关系” ．

（本小题满分12分）在最近发生的飞机失联事件中，各国竭尽全力搜寻相关信息，为体现国际共产主义援助精神，中国海监某支队奉命搜寻某海域。若该海监支队共有、型两种海监船10艘，其中型船只7艘，型船只3艘。
（1）现从中任选2艘海监船搜寻某该海域，求恰好有1艘型海监船的概率；
（2）假设每艘型海监船的搜寻能力指数为5，每艘型海监船的搜寻能力指数为10．现从这10艘海监船中随机的抽出4艘执行搜寻任务，设搜寻能力指数共为，求的分布列及期望．

已知随机变量X的方差V（X）=1，设随机变量Y=2X+3，则V（Y）=       ．