(本小题满分13分)为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
| 队别 |
北京 |
上海 |
天津 |
八一 |
| 人数 |
4 |
6 |
3 |
5 |
(Ⅰ)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(Ⅱ)中国女排奋力拼搏,战胜韩国队获得冠军.若要求选出两位队员代表发言,设其中来自北京队
的人数为 ,求随机变量
,求随机变量 的分布列,及数学期望
的分布列,及数学期望 .
.
相关知识点
推荐套卷
 ,
,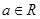 .
. 时,求函数
时,求函数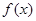 的最大值的表达式
的最大值的表达式 .
. ,使得
,使得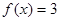 有且仅有3个不等实根,且它们成等差数列,若存在,求出所有
有且仅有3个不等实根,且它们成等差数列,若存在,求出所有 的方程为
的方程为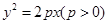 ,点
,点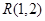 在抛物线
在抛物线
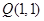 作直线交抛物线
作直线交抛物线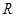 的两点
的两点 ,
,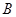 ,若直线
,若直线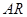 ,
,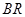 分别交直线
分别交直线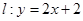 于
于 ,
, 两点,求
两点,求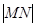 最小时直线
最小时直线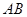 的方程.
的方程. 中,
中, 平面
平面 ,
, ,点
,点 ,
, 分别为
分别为 ,
, 的中点.
的中点.
 平面
平面 ;
; 在线段
在线段 上的点,且
上的点,且 平面
平面 .
. 与平面
与平面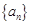 的前
的前 项和为
项和为 ,且
,且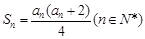 .
. ,求数列
,求数列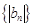 的前
的前 项和.
项和. ,
,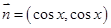 ,若函数
,若函数 .
.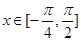 时,函数
时,函数 的值域;
的值域; 中,
中,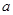 ,
,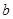 ,
,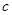 分别是角
分别是角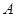 ,
,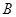 ,
, 的对边,若
的对边,若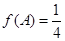 且
且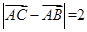 ,求
,求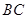 边上中线长的最大值.
边上中线长的最大值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号