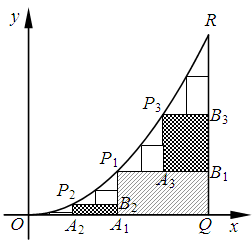
如图,已知曲线C:y=x2(0≤x≤1),O(0,0),Q(1,0),R(1,1).取线段OQ的中点A1,过A1作x轴的垂线交曲线C于P1,过P1作y轴的垂线交RQ于B1,记a1为矩形A1P1B1Q的面积.分别取线段OA1,P1B1的中点A2,A3,过A2,A3分别作x轴的垂线交曲线C于P2,P3,过P2,P3分别作y轴的垂线交A1P1,RB1于B2,B3,记a2为两个矩形A2P2B2 A1与矩形A3P3B3B1的面积之和.以此类推,记an为2n-1个矩形面积之和,从而得数列{an},设这个数列的前n项和为Sn.
(I)求a2与an;
(Ⅱ)求Sn,并证明Sn<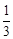 .
.