（本小题满分12分）在最近发生的飞机失联事件中，各国竭尽全力搜寻相关信息，为体现国际共产主义援助精神，中国海监某支队奉命搜寻某海域。若该海监支队共有
、
型两种海监船10艘，其中型船只7艘，型船只3艘。
（1）现从中任选2艘海监船搜寻某该海域，求恰好有1艘型海监船的概率；
（2）假设每艘型海监船的搜寻能力指数为5，每艘型海监船的搜寻能力指数为10．现从这10艘海监船中随机的抽出4艘执行搜寻任务，设搜寻能力指数共为
，求的分布列及期望．
相关试题
附加题（本大题共两个小题，每个小题10分，满分 20分，省级示范性高中要
把该题成绩计入总分，普通高中学生选作）
已知
，
（1）判断函数在区间（-∞，0）上的单调性，并用定义证明；
（2）画出该函数在定义域上的图像.（图像体现出函数性质即可）
(本题满分10分)
某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需维护费150元,未租出的车每月需维护费50元.
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大
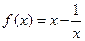月收益为多少？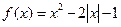
的图像，并写出该函数的单调区间与值域.
本题满分10分）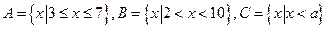
。
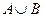；（2）求
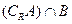；（3）若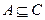
，求a的取值范围.
题满分10分)化简或求值： 
；
.相关知识点
推荐套卷
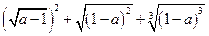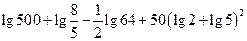粤公网安备 44130202000953号