附加题（本大题共两个小题，每个小题10分，满分 20分，省级示范性高中要
把该题成绩计入总分，普通高中学生选作）
已知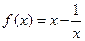
，
（1）判断函数在区间（-∞，0）上的单调性，并用定义证明；
（2）画出该函数在定义域上的图像.（图像体现出函数性质即可）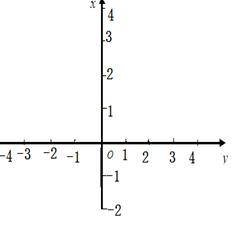
相关试题
和400π
，其中
时，判断函数
在定义域上的单调性；
，不等式
都成立。
的前n项和为
，且
。
是等比数列；
满足
，且
，求数列
。
的最小正周期及在区间
上的最大值和最小值；
，
，求
的值。
，
，其中
，a、b为常数，已知曲线
在点（2,0）处有相同的切线
。
单调区间与极值。相关知识点
推荐套卷
附加题（本大题共两个小题，每个小题10分，满分 20分，省级示范性高中要
把该题成绩计入总分，普通高中学生选作）
已知，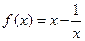
（1）判断函数在区间（-∞，0）上的单调性，并用定义证明；
（2）画出该函数在定义域上的图像.（图像体现出函数性质即可）
粤公网安备 44130202000953号