北京市东城区高三5月综合练习二理科数学试卷
甲、乙两名同学 次数学测验成绩如茎叶图所示,
次数学测验成绩如茎叶图所示,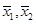 分别表示甲、乙两名同学
分别表示甲、乙两名同学 次数学测验成绩的平均数,
次数学测验成绩的平均数, 分别表示甲、乙两名同学
分别表示甲、乙两名同学 次数学测验成绩的标准差,则有( )
次数学测验成绩的标准差,则有( )
A. , , |
B.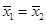 , , |
C.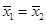 , ,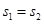 |
D.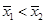 , ,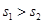 |
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
已知 ,
, 是简单命题,那么“
是简单命题,那么“ 是真命题”是“
是真命题”是“ 是真命题”的( )
是真命题”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为 ,其中
,其中 (
( ),传输信息为
),传输信息为 ,
, ,
, ,
, 运算规则为:
运算规则为: ,
, ,
, ,
, .例如原信息为
.例如原信息为 ,则传输信息为
,则传输信息为 .传播信息在传输过程中受到干扰可能导致接收信息出错,则下列信息一定有误的是( )
.传播信息在传输过程中受到干扰可能导致接收信息出错,则下列信息一定有误的是( )
A. |
B. |
C. |
D. |
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
如图,平面中两条直线 和
和 相交于点
相交于点 ,对于平面上任意一点
,对于平面上任意一点 ,若
,若 分别是
分别是 到直线
到直线 和
和 的距离,则称有序非负实数对
的距离,则称有序非负实数对 是点
是点 的“距离坐标”.
的“距离坐标”.
给出下列四个命题:
① 若 ,则“距离坐标”为
,则“距离坐标”为 的点有且仅有
的点有且仅有 个.
个.
② 若 ,且
,且 ,则“距离坐标”为
,则“距离坐标”为 的点有且仅有
的点有且仅有 个.
个.
③ 若 ,则“距离坐标”为
,则“距离坐标”为 的点有且仅有
的点有且仅有 个.
个.
④ 若 ,则点
,则点 的轨迹是一条过
的轨迹是一条过 点的直线.
点的直线.
其中所有正确命题的序号为 .
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
某校高一年级开设 ,
, ,
, ,
, ,
, 五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选
五门选修课,每位同学须彼此独立地选三门课程,其中甲同学必选 课程,不选
课程,不选 课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
课程,另从其余课程中随机任选两门课程.乙、丙两名同学从五门课程中随机任选三门课程.
(Ⅰ)求甲同学选中 课程且乙同学未选中
课程且乙同学未选中 课程的概率;
课程的概率;
(Ⅱ)用 表示甲、乙、丙选中
表示甲、乙、丙选中 课程的人数之和,求
课程的人数之和,求 的分布列和数学期望.
的分布列和数学期望.
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
如图,三棱柱 的侧面
的侧面 是边长为
是边长为 的正方形,侧面
的正方形,侧面 侧面
侧面 ,
, ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)在线段 上是否存在一点
上是否存在一点 ,使二面角
,使二面角 为
为 ,若存在,求
,若存在,求 的长;若不存在,说明理由.
的长;若不存在,说明理由.
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
已知椭圆 的中心在原点
的中心在原点 ,焦点在
,焦点在 轴上,离心率为
轴上,离心率为 ,且椭圆
,且椭圆 上的点到两个焦点的距离之和为
上的点到两个焦点的距离之和为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设 为椭圆
为椭圆 的左顶点,过点
的左顶点,过点 的直线
的直线 与椭圆交于点
与椭圆交于点 ,与
,与 轴交于点
轴交于点 ,过原点与
,过原点与 平行的直线与椭圆交于点
平行的直线与椭圆交于点 .证明:
.证明: .
.
来源:2015届北京市东城区高三5月综合练习二理科数学试卷
 ( )
( )



 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系是( )
的大小关系是( )



 为各项都是正数的等比数列,若
为各项都是正数的等比数列,若 ,则
,则 ( )
( )



 满足不等式组
满足不等式组 则
则 的取值范围是( )
的取值范围是( )



 上的函数
上的函数 满足
满足 .当
.当 时,
时, ,当
,当 时,
时, ,则
,则 ( )
( )



 的二项展开式中各项的二项式系数的和是
的二项展开式中各项的二项式系数的和是 ,则
,则 ,展开式中的常数项为 .(用数字作答)
,展开式中的常数项为 .(用数字作答) 满足
满足 ,那么
,那么 的最小值为 .
的最小值为 . 为参数
为参数 与曲线
与曲线 为参数,
为参数,
 .
. 截抛物线
截抛物线 的准线所得线段长为
的准线所得线段长为 ,则
,则 .
. 满足
满足 ,
, 与
与 的夹角为
的夹角为 ,则
,则 的取值范围是 .
的取值范围是 . .
. 的定义域及其最大值;
的定义域及其最大值; 上的单调递增区间.
上的单调递增区间. .
. 时,求
时,求 在区间
在区间 上的最小值;
上的最小值; ,有
,有 .
. 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, ,设
,设 ,
, .
. 是等比数列;
是等比数列; ,
, 的最小值;
的最小值; 时,给出一个新数列
时,给出一个新数列 ,其中
,其中 设这个新数列的前
设这个新数列的前 ,若
,若 (
( 且
且 )的形式,则称
)的形式,则称 中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由.
中的项是否存在“指数型和”,若存在,求出所有“指数型和”;若不存在,请说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号