在四棱锥 中,
中, 平面
平面 ,
, 是正三角形,
是正三角形, 与
与 的交点
的交点 恰好是
恰好是 中点,又
中点,又 ,
, ,点
,点 在线段
在线段 上,且
上,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(本小题满分14分)
在如图所示的几何体中,四边形 为正方形,
为正方形, 平面
平面 ,
, ,
, .
.
(Ⅰ)若点 在线段
在线段 上,且满足
上,且满足 ,求证:
,求证: 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的余弦值.
的余弦值.
(本小题满分12分)如图所示,正方体ABCD-A1B1C1D1中,P、Q分别是AD1、BD上的点,且AP=BQ,求证:PQ∥平面DCC1D1.
(本小题满分12分)如图,四棱锥P ABCD中,底面ABCD为平行四边形, ,PA⊥平面ABCD,E为PD的中点.
,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设AD=2, ,求点
,求点 到平面
到平面 的距离.
的距离.
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)如图,四棱锥 中,
中, 是正三角形,四边形
是正三角形,四边形 是矩形,且平面
是矩形,且平面
 平面
平面 ,
, ,
, .
.
(Ⅰ)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(Ⅱ)若点 在线段
在线段 上,且
上,且 ,当三棱锥
,当三棱锥 的体积为
的体积为 时,求实数
时,求实数 的值.
的值.
如图,在三棱台
中,
分别为
的中点.

(Ⅰ)求证:
平面
;
(Ⅱ)若
平面
,
,
,求平面
与平面
所成的角(锐角)的大小.
(本小题只理科做,满分14分)如图,已知 平面
平面 ,
, ,△
,△ 是正三角形,
是正三角形, ,且
,且 是
是 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求平面 与平面
与平面 所成锐二面角的大小.
所成锐二面角的大小.
如图,直三棱柱 中,D,E分别是AB,
中,D,E分别是AB, 的中点
的中点
(1)证明: ;
;
(2)设 ,求三棱锥
,求三棱锥 的体积
的体积
如图,三角形
所在的平面与长方形
所在的平面垂直,
,
,
.

(1)证明:
平面
;
(2)证明:
;
(3)求点
到平面
的距离.
己知四棱锥P-ABCD,其中底面ABCD为矩形侧棱PA 底面ABCD,其中BC=2,AB=2PA=6,
底面ABCD,其中BC=2,AB=2PA=6,
M,N为侧棱PC上的两个三等分点,如图所示: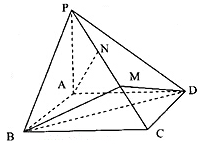
(1)求证:AN∥平面MBD;
(2)求二面角B-PC-A的余弦值.
(本小题满分14分)如图,菱形 的边长为
的边长为 ,
, ,
, .将菱形
.将菱形 沿对角线
沿对角线 折起,得到三棱锥
折起,得到三棱锥 ,点
,点 是棱
是棱 的中点,
的中点, .
.
(1)求证: 平面
平面 ;
;
(2)求三棱锥 的体积.
的体积.
如图所示,在多面体 ,四边形 , 均为正方形, 为 的中点,过 的平面交 于 .
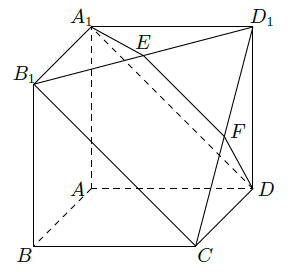
(Ⅰ)证明:
;
(Ⅱ)求二面角
余弦值.