(本小题满分12分)如图,四棱锥P ABCD中,底面ABCD为平行四边形, ,PA⊥平面ABCD,E为PD的中点.
,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设AD=2, ,求点
,求点 到平面
到平面 的距离.
的距离.
(本小题满分12分)如图,在四棱锥 中,底面
中,底面 为直角梯形,且
为直角梯形,且 ,
, ,侧面
,侧面 底面
底面 . 若
. 若 .
. (1)求证:
(1)求证: 平面
平面 ;
;
(2)侧棱 上是否存在点
上是否存在点 ,使得
,使得 平面
平面 ?若存在,指出点
?若存在,指出点 的位置并证明;若不存在,请说明理由。
的位置并证明;若不存在,请说明理由。
如图,三棱柱ABC﹣A1B1C1的底面是边长为3的正三角形,侧棱AA1垂直于底面ABC,AA1= ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.
(1)求证:直线BC1∥平面AB1D;
(2)求三棱锥C1﹣ABB1的体积.
如图,矩形ABCD所在的平面与三角形CDE所在的平面交于CD, AE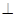 平面CDE.
平面CDE.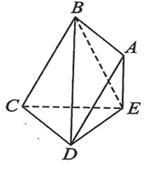
求证:(1)AB//平面CDE;
(2)CD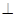 平面ADE.
平面ADE.
(本小题满分12分)如图是三棱柱 的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形,
的三视图,正(主)视图和俯视图都是矩形,侧(左)视图为等边三角形, 为
为 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)设 垂直于
垂直于 ,求二面角
,求二面角 的大小.
的大小.
如图,四棱锥 的底面
的底面 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面 ,
, ,
, 是
是 的中点.
的中点.
(Ⅰ)证明: //平面
//平面 ;
;
(Ⅱ)求二面角 的平面角的余弦值;
的平面角的余弦值;
(Ⅲ)在棱 上是否存在点
上是否存在点 ,使
,使 ⊥平面
⊥平面 ?证明你的结论.
?证明你的结论.
如图,四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 是
是 的中点.
的中点.
(1)证明: 平面
平面 ;
;
(2)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
如图,直三棱柱ABC﹣A1B1C1中,AC⊥BC,AC=BC=CC1=2,M,N分别为AC,B1C1的中点.
(Ⅰ)求证:MN∥平面ABB1A1;
(Ⅱ)线段CC1上是否存在点Q,使A1B⊥平面MNQ?说明理由.
在如图所示的几何体中,四边形 是菱形,
是菱形, 是矩形,平面
是矩形,平面 ⊥平面
⊥平面 ,
, 是
是 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)在线段 上是否存在点
上是否存在点 ,使二面角
,使二面角 的大小为
的大小为 ?若存在,求出
?若存在,求出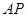 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
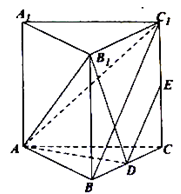
如图,已知直三棱柱 中,
中, ,
, 、
、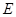 分别为
分别为 、
、 中点,
中点, .
.
(1)求证: 平面
平面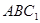 ;
;
(2)求证:平面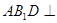 平面
平面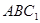
在如图所示的几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF//AB,AF⊥CF.
(1)若G为FC的中点,证明:AF//平面BDG;
(2)求平面ABF与平面BCF夹角的余弦值.
如图,在三棱柱 中,
中, 底面
底面 ,
, ,点
,点 是
是 的中点.
的中点.

(Ⅰ)求证: ;
;
(Ⅱ)求证: ∥平面
∥平面 .
.
(Ⅲ)设 ,
, ,在线段
,在线段 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,确定点
?若存在,确定点 的位置; 若不存在,说明理由.
的位置; 若不存在,说明理由.