(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.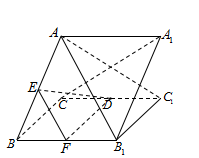
(1)求证:平面AB1C1⊥平面AC1;
(2)若AB1⊥A1C,求线段AC与AA1长度之比;
(3)若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.
推荐套卷
(本小题满分12分)如图所示,在直三棱柱ABC-A1B1C1中,AC⊥BC.
(1)求证:平面AB1C1⊥平面AC1;
(2)若AB1⊥A1C,求线段AC与AA1长度之比;
(3)若D是棱CC1的中点,问在棱AB上是否存在一点E,使DE∥平面AB1C1?若存在,试确定点E的位置;若不存在,请说明理由.