在如图所示的几何体中,四边形ABCD为矩形,AB=2BC=4,BF=CF=AE=DE,EF=2,EF//AB,AF⊥CF.
(1)若G为FC的中点,证明:AF//平面BDG;
(2)求平面ABF与平面BCF夹角的余弦值.
设 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,有以下四个命题:
是三个不同的平面,有以下四个命题:
① ②
② ③
③ ④
④
其中正确的命题是( )
| A.①④ | B.②③ | C.①③ | D.②④ |
如图,已知四棱锥 ,
,  ,
,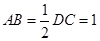 ,
,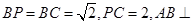 平面
平面 ,
,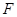 为
为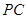 中点.
中点.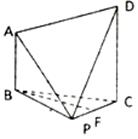
(Ⅰ)求证: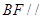 平面
平面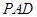 ;
;
(Ⅱ)求证:平面 平面
平面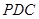 .
.
如图:已知正方形ABCD的边长为2,且AE⊥平面CDE,AD与平面CDE所成角为 .
.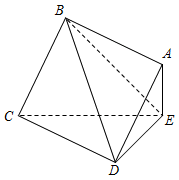
(1)求证:AB∥平面CDE;
(2)求三棱锥D-ACE的体积.
设l,m是不同的直线,α,β,γ是不同的平面,则下列命题正确的是______________.
①若l⊥m,m⊥α,则l⊥α或 l∥α
②若l⊥γ,α⊥γ,则l∥α或 l α
α
③若l∥α,m∥α,则l∥m或 l与m相交
④若l∥α,α⊥β,则l⊥β或l β
β
如图所示,已知ABCD为梯形,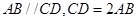 ,且
,且 ,
, 为线段PC上一点.
为线段PC上一点.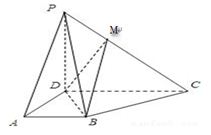
(1)当 时,证明:
时,证明: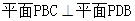 ;
;
(2)设平面 ,证明:
,证明:
(3)在棱PC上是否存在点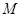 ,使得
,使得 ,若存在,请确定点
,若存在,请确定点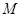 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.