高中数学平行线法试题

（本小题满分12分）如图，内接于圆O，AB是圆O的直径，，，，四边形DCBE为平行四边形，平面ABC.

（1）证明：平面平面ADE；
（2）在CD上是否存在一点M，使得平面ADE？证明你的结论.

给出四个命题：
①平行于同一平面的两个不重合的平面平行；
②平行于同一直线的两个不重合的平面平行；
③垂直于同一平面的两个不重合的平面平行；
④垂直于同一直线的两个不重合的平面平行；
其中真命题的序号是________．

如图，在三棱柱中，底面，，点是的中点． 

（Ⅰ）求证：；
（Ⅱ）求证：∥平面．
（Ⅲ）设，，在线段上是否存在点，使得?若存在，确定点的位置;                         若不存在，说明理由．

如图，在四棱锥中，侧棱⊥底面，，，，，是棱的中点．

（1）求证：面；
（2）设点是线段上的一点，且在方向上的射影为，记与面所成的角为，问：为何值时，取最大值？

如图，在四棱锥P-ABCD中，，，，，，E为PD的中点．

求证：（1）平面PBC；
（2）平面ACE．

如图，矩形ABCD所在的平面与三角形CDE所在的平面交于CD, AE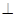平面CDE．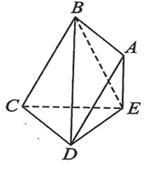

求证：（1）AB//平面CDE;
（2）CD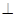平面ADE．

在三棱柱中,平面,且,,为中点, 则点在线段上运动时, 可能出现

A．平面	B．平面
C．平面	D．平面

在如图所示的几何体中，四边形ABCD为矩形，AB=2BC=4，BF=CF=AE=DE，EF=2，EF//AB，AF⊥CF。

（Ⅰ）若G为FC的中点，证明：AF//平面BDG；
（Ⅱ）求平面ABF与平面BCF夹角的余弦值。

下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB//平面MNP的图形是（   ）

A．①②      B．①④      C．②③     D．③④

如图，四边形ABCD为平行四边形，四边形ADEF是正方形，且BD⊥平面CDE，H是BE的中点，G是AE，DF的交点．

（1）求证：GH∥平面CDE；
（2）求证：面ADEF⊥面ABCD．

（本小题满分14分）如图,已知四边形是正方形,平面,//,,,,分别为,,的中点．
（Ⅰ）求证:平面FGH //平面;
（Ⅱ）求证:平面平面;
（Ⅲ）在线段上是否存在一点,使平面?若存在,求出线段的长;若不存在,请说明理由．

（本小题满分12分）如图，四棱锥S—ABCD中，底面ABCD是菱形，其对角线的交点为O，且SA＝SC，SA⊥BD
（1）求证：SO⊥平面ABCD；
（2）设∠BAD＝60°，AB＝SD＝2，P是侧棱SD上的一点，且SB∥平面APC，求三棱锥A—PCD的体积．

（本小题满分12分）如图所示，正方体ABCD－A₁B₁C₁D₁中，P、Q分别是AD₁、BD上的点，且AP＝BQ，求证：PQ∥平面DCC₁D₁．

如图，AB为圆O的直径，点C在圆周上（异于点A，B），直线PA垂直于圆O所在的平面，点M为线段PB的中点．有以下四个命题：
①PA∥平面MOB；      ②OC⊥平面PAC；
③MO∥平面PAC；      ④平面PAC⊥平面PBC．
其中正确的命题是（ ）．

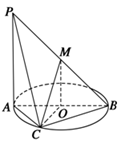
A．①②       B．①③       C．③④        D．②④

若直线与平行，则它们之间的距离为          ．