高中数学误差估计解答题

在某中学举行的数学知识竞赛中，将三个年级参赛学生的成绩在进行整理后分成
5组，绘制出如图所示的频率分布直方图，图中从左到右依次为第一、第二、第三、第四、
第五小组。已知第三小组的频数是15。
（1）求成绩在50—70分的频率是多少；
（2）求这三个年级参赛学生的总人数是多少；
（3）求成绩在80—100分的学生人数是多少；   
    

（本小题满分12分）
为备战2012奥运会，甲、乙两位射击选手进行了强化训练. 现分别从他们的强化训练期间的若干次平均成绩中随机抽取8次，记录如下：
甲：8.3，9.0，7.9，7.8，9.4，8.9，8.4，8.3；
乙：9.2，9.5，8.0，7.5，8.2，8.1，9.0，8.5.
（1）画出甲、乙两位选手成绩的茎叶图；(用茎表示成绩的整数部分，用叶表示成绩的小数部分)
（2）现要从中选派一人参加奥运会，从平均成绩和发挥稳定性角度考虑，你认为派哪位选手参加合理? 简单说明理由.
（3）若将频率视为概率，对选手乙在今后的三次比赛成绩进行预测，记这三次成绩中不低于8.5分的次数为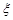，求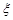的分布列及均值E.

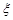从全校参加数学竞赛的学生的试卷中抽取一个样本，考察竞赛的成绩分布，将样本分成5组，绘成频率分布直方图，图中从左到右各小组的小长方形的高之比为1:3:6:4:2，最右边一组的频数是6，请结合直方图提供的信息，解答下列问题：

(1)样本的容量是多少？
(2)列出频率分布表；
(3)成绩落在哪个范围内的人数最多？并求出该小组的频数，频率；
(4)估计这次竞赛中，成绩高于60分的学生占总人数的百分比.

下图是总体的一样本频率分布直方图,且在［15,18)内频数为8.
(1)求样本容量;
(2)若在［12,15)内小矩形面积为0.06,求在［12,15)内频数;
(3)在（2）的条件下，求样本在［18,33)内的频率.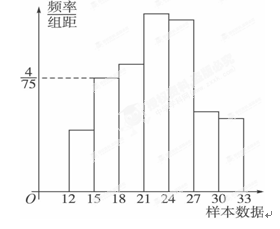

（本小题满分13分）对某校高一年级的学生参加社区服务的次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数，根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图：

（I）求出表中M、p及图中a的值
（II）学校决定对参加社区服务的学生进行表彰，对参加活动次数在［25，30］区间的每个学生发放价值80元的学习用品，对参加活动次数在［20,25）区间的每个学生发放价值60元的学习用品，对参加活动次数在［15,20）区间的每个学生发放价值40元的学习用品，对参加活动次数在［10,15）区间的每个学生发放价值20元的学习用品，在所抽取的这M名学生中，任意取出2人，设X为此二人所获得学习用品价值之差的绝对值，求X的分布列与数学期望E（X）。

(本小题满分12分)某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组：第1组[160，165)，第2组[165，170)，第3组[170，175)，第4组[175，180)，第5组[180，185)得到的频率分布直方图如图所示。

(Ⅰ)求第3、4、5组的频率；
(Ⅱ)为了能选拔出最优秀的学生，该校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试?
(Ⅲ)在(Ⅱ)的前提下，学校决定在这6名学生中随机抽取2名学生接受甲考官的面试，求：第4组至少有一名学生被甲考官面试的概率?

甲乙两名自行车赛手在相同条件下进行了6次测试，测得最大速度数据如下：

甲	27	38	30	37	35	31
乙	33	29	38	34	28	36

请解答：（1）画茎叶图                
（2）求甲乙两组数据的中位数、平均数和标准差并判断谁参加比赛更合适

2010年上海世博会举办时间为2010年5月1日--10月31日．此次世博会福建馆招募了60名志愿者，某高校有13人入选，其中5人为中英文讲解员，8人为迎宾礼仪，它们来自该校的5所学院（这5所学院编号为1、2、3、4、5号），人员分布如图所示． 若从这13名入选者中随机抽出3人．

（1）求这3人所在学院的编号正好成等比数列的概率；
（2）求这3人中中英文讲解员人数的分布列及数学期望．

某高中三年级有一个实验班和一个对比班，各有50名同学．根据这两个班市二模考试的数学科目成绩（规定考试成绩在[120，150]内为优秀），统计结果如下：
实验班数学成绩的频数分布表：
对比班数学成绩的频数分布表：

（Ⅰ）分别求这两个班数学成绩的优秀率；若采用分层抽样从实验班中抽取15位同学的数学试卷，进行试卷分析，则从该班数学成绩为优秀的试卷中应抽取多少份?
（Ⅱ）统计学中常用M值作为衡量总体水平的一种指标，已知M与分数t的关系式为：

分别求这两个班学生数学成绩的M总值，并据此对这两个班数学成绩总体水平作一简单评价．

某校从参加高一年级期中考试的学生中随机抽取名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：

(Ⅰ)求分数在内的频率，并补全这个频率分布直方图；
（Ⅱ）用分层抽样的方法在分数段为的学生中抽取一个容量为的样本，
将该样本看成一个总体，从中任取人，求至多有人在分数段的概率.

某工厂对某产品的产量与成本的资料分析后有如下数据：

产量x千件	2	3	5	6
成本y万元	7	8	9	12

 (Ⅰ) 画出散点图.
(Ⅱ) 求成本y与产量x之间的线性回归方程.

我国是世界上严重缺水的国家之一，城市缺水问题较为突出.某市为了节约生活用水，计划在本市试行居民生活用水定额管理（即确定一个居民月均用水量标准〜用水量不超过a的部分按照平价收费，超过a的部分按照议价收费）.为了较为合理地确定出这个标准，通过抽样获得了 100位居民某年的月均用水量(单位:t)，制作了频率分布直方图，
(I)由于某种原因频率分布直方图部分数据丢失，请在图中将其补充完整；
(II)用样本估计总体，如果希望80%的居民每月的用水量不超出标准&则月均用水量的最低标准定为多少吨，并说明理由；
(III)若将频率视为概率，现从该市某大型生活社区随机调查3位居民的月均用水量(看作有放回的抽样），其中月均用水量不超过（II)中最低标准的人数为x，求x的分布列和均值.

2011年3月5日某校组织同学听取了温家宝总理所作的政府工作报告，并进行了检测，从参加检测的高一学生中随机抽出60名学生，将其成绩(均为整数)分成六段［40,50),［50,60),…,［90,100］后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：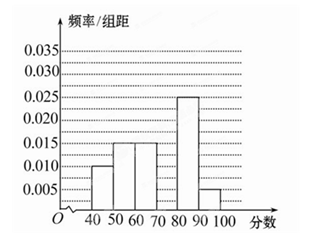

（Ⅰ）求分数在［70,80)内的频率，并补全这个频率分布直方图；
（Ⅱ）请根据频率分布直方图估计本次考试中的成绩的平均分及中位数（可保留一位小数）.

电视传媒公司为了了解某地区电视观众对某类体育节目的收视情况，随机抽取了100名观众进行调查，其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图；

将日均收看该体育节目时间不低于40分钟的观众称为"体育迷"，已知"体育迷"中有10名女性。
(Ⅰ)根据已知条件完成下面的2×2列联表，并据此资料你是否认为"体育迷"与性别有关？

	非体育迷	体育迷	合计
男
女
合计

(Ⅱ)将日均收看该体育项目不低于50分钟的观众称为"超级体育迷"，已知"超级体育迷"中有2名女性，若从"超级体育迷"中任意选取2人，求至少有1名女性观众的概率。

$P(x^2\ge k)$	0.05	0.01
$k$	3.841	6.635

附 $X^2=\frac{n(n_{11}{n}_{22}-n_{12}{n}_{21}{)}^2}{n_{1+}{n}_{2+}{n}_{+1}{n}_{+2}}$

某校从参加高三年级理科综合物理考试的学生中随机抽出名学生，将其数学成绩（均为整数）分成六段，…后得到如下部分频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）求分数在内的频率，并补全这个频率分布直方图；
（Ⅱ）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的
平均分；
（Ⅲ）若从名学生中随机抽取人，抽到的学生成绩在记分，在记分，
在记分，用表示抽取结束后的总记分，求的分布列和数学期望.