有100株玉米,其单株产量的频率分布表如下:
| 单株玉米产量区间(千克) |
频数 |
频率 |
 |
7 |
0.07 |
 |
13 |
0.13 |
 |
20 |
0.20 |
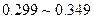 |
25 |
0.25 |
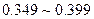 |
22 |
0.22 |
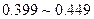 |
7 |
0.07 |
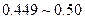 |
6 |
0.06 |
(1)画出单株产量的频率分布直方图;
(2)用极限的观点说明玉米单株产量 的概率密度曲线及概率密度函数的得出.
的概率密度曲线及概率密度函数的得出.
从两个班中各随机的抽取 名学生,他们的数学成绩如下:
名学生,他们的数学成绩如下:
| 甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
78 |
72 |
52 |
68 |
| 乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
82 |
74 |
88 |
85 |
画出茎叶图并分析两个班学生的数学学习情况。
对某校初二男生抽取体育项目俯卧撑,被抽到的 名学生的成绩如下:
名学生的成绩如下:
| 成绩(次) |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
| 人数 |
8 |
6 |
5 |
16 |
4 |
7 |
3 |
1 |
试求全校初二男生俯卧撑的平均成绩。
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示。
(1)求这次测试数学成绩的众数;
(2)求这次测试数学成绩的中位数;
(3)求这次测试数学成绩的平均分。
下图是某市有关部门根据对某地干部的月收入情况调查后画出的样本频率分布直方图,已知图中第一组的频数为4000.请根据该图提供的信息解答下列问题:(图中每组包括左端点,不包括右端点,如第一组表示收入在 )
)
(1)求样本中月收入在 的人数;
的人数;
(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本的各组中按月收入再用分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人?
(3)试估计样本数据的中位数.
(本小题满分14分)

为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
潮州统计局就某地居民的月收入调查了 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在 )。
)。
(1)求居民月收入在 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这 人中用
人中用
分层抽样方法抽出 人作进一步分析,则月收入在
人作进一步分析,则月收入在 的这段应抽多少人?
的这段应抽多少人?
某种家用电器每台的销售利润与该电器的无故障使用时间T (单位:年)有关.若T≤1,则销售利润为0元;若1<T≤3,则销售利润为100元;若T>3,则销售利润为200元.设每台该种电器的无故障使用时间T≤1,1<T≤3及T>3这三种情况发生的概率分别为p1,p2,p3,又知p1,p2是方程 的两个根,且p2=p3.
的两个根,且p2=p3.
(1)求p1,p2,p3的值;
(2)记 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 的期望.
的期望.
(本小题满分12分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:
若将频率视为概率,回答下列问题.(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率; (Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及Eξ.