(本小题满分14分)
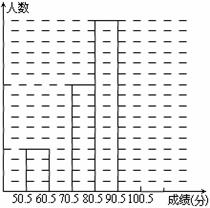
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题:
(1)填充频率分布表的空格(将答案直接填在表格内);
(2)补全频数条形图;
(3)若成绩在75.5~85.5分的学生为二等奖,问获得二等奖的学生约为多少人?
相关知识点
推荐套卷
 中,
中,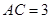 ,
, ,
,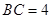 .
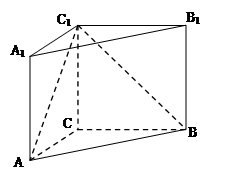
.
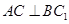 ;
;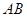 线段上存在一点
线段上存在一点 ,使得
,使得 平面
平面 ?若存在,请证明;若不存在,请说明理由.
?若存在,请证明;若不存在,请说明理由. 是各项均不为零的等差数列,公差为
是各项均不为零的等差数列,公差为 ,
, 为其前
为其前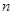 项和,且满足
项和,且满足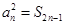 ,
, .数列
.数列 满足
满足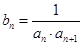 ,
, 为数列
为数列 和
和 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 中,角
中,角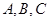 的对边分别为
的对边分别为 ,且
,且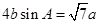 .
.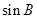 的值;
的值; 的值.
的值.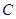 :
: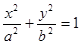
 ,
, ,求椭圆的标准方程;
,求椭圆的标准方程; 的直线
的直线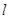 与椭圆
与椭圆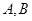 ,且
,且 为锐角(
为锐角(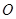 为坐标原点),求直线
为坐标原点),求直线 的取值范围;
的取值范围; 四点,设原点
四点,设原点 的一边距离为
的一边距离为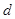 ,试求
,试求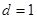 时
时 满足的条件.
满足的条件. 的全体:存在非零常数T,对任意
的全体:存在非零常数T,对任意 ∈R,有
∈R,有 成立.
成立. 是否属于集合M?说明理由;
是否属于集合M?说明理由; ,求证:
,求证: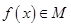 ;
;  且
且 )的图象与
)的图象与 的图象有公共点,证明:
的图象有公共点,证明: ∈M;
∈M; 粤公网安备 44130202000953号
粤公网安备 44130202000953号