从两个班中各随机的抽取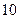 名学生,他们的数学成绩如下:
名学生,他们的数学成绩如下:
| 甲班 |
76 |
74 |
82 |
96 |
66 |
76 |
78 |
72 |
52 |
68 |
| 乙班 |
86 |
84 |
62 |
76 |
78 |
92 |
82 |
74 |
88 |
85 |
画出茎叶图并分析两个班学生的数学学习情况。
相关知识点
推荐套卷
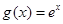 ,
, ,其中
,其中 是常数,且
是常数,且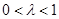 .
. 的极值;
的极值;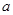 ,存在正数
,存在正数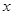 ,使不等式
,使不等式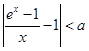 成立;
成立; ,且
,且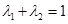 ,证明:对任意正数
,证明:对任意正数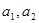 都有:
都有: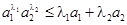 .
. 的首项
的首项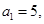 前
前 项和为
项和为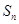 ,且
,且
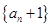 是等比数列;
是等比数列;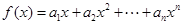 ,求函数
,求函数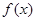 在点
在点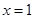 处的导数
处的导数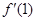 ,并比较
,并比较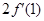 与
与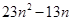 的大小.
的大小.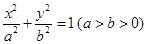 的左右顶点分别为
的左右顶点分别为 ,离心率
,离心率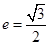 .过该椭圆上任一点
.过该椭圆上任一点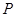 作
作 轴,垂足为
轴,垂足为 ,点
,点 在
在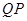 的延长线上,且
的延长线上,且 .
. 的方程;
的方程; (
( )与直线
)与直线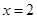 交于点
交于点 ,
,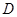 为线段
为线段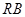 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线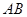 为圆
为圆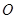 的直径,点
的直径,点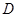 为线段
为线段 ,点
,点 为圆
为圆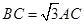 .点
.点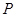 在圆
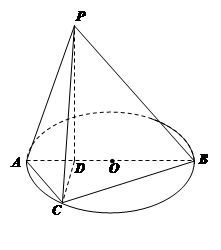
在圆 .
.
 ;
;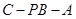 的余弦值.
的余弦值.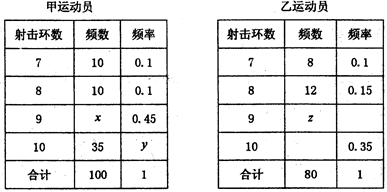
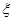 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求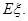
 粤公网安备 44130202000953号
粤公网安备 44130202000953号