高中数学误差估计解答题

国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：

由全国重点城市环境监测网获得2月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图：

（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s²=[（x₁﹣）²+（x₂﹣）²+…+（x_n﹣）²]，其中为数据x₁，x₂，…，x_n的平均数．）

2015年五一节”期间，高速公路车辆“较多，交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度，采用的方法是：按到达监控点先后顺序，每隔50辆抽取一辆，总共抽取120辆，分别记下其行车速度，将行车速度（km/h）分成七段[60，65），[65，70），[70，75），[75，80），[80，85），[85，90），[90，95）后得到如图所示的频率分布直方图，据图解答下列问题：

（1）求a的值，并说明交警部门采用的是什么抽样方法？
（2）若该路段的车速达到或超过90km/h即视为超速行驶，试根据样本估计该路段车辆超速行驶的概率；
（3）求这120辆车行驶速度的众数和中位数的估计值（精确到0．1）。

某地区为了了解某地区高中生的身体发育情况，对某一中学的随机抽取的50名学生的体重进行了测量，结果如下：（单位：kg）
42,38,29,36,41,43,54,43,34,44,40,59,39,42,44,50,37,44,45,29,48,45,53,48,37,28,46,50,37,44,
42,39,51,52,62,47,59,46,45,,67,53，49,65,47,54,63,58,43,46,58.

分组	频数	频率	频率/组距
[27,32)		0.06
[32,37)		0.06
[37,42)	9
[42,47)			0.064
[47,52)	7
[52,57)	5
[57,62)	4
[62,67)		0.06

 
（1）若以组距为5，完成下面样本频率分布表：
（2）根据（1）中的频率分布表，画出频率分布直方图；
（3）若本地区学生总人数为3000人，试根据抽样比例，估计本地区学生体重在区间[37,57]内所占的人数约为多少人？

为了了解小学五年级学生的体能情况，抽取了实验小学五年级部分学生进行踢毽子测试，将所得的数据整理后画出频率分布直方图（如图），已知图中从左到右的前三个小组的频率分别是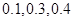，第一小组的频数是．

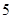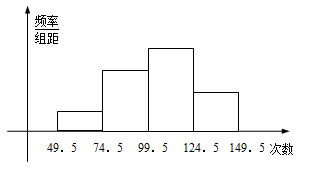
（Ⅰ）求第四小组的频率和参加这次测试的学生人数；
（Ⅱ）在这次测试中，问学生踢毽子次数的中位数落在第几小组内？
（Ⅲ）在这次跳绳测试中，规定跳绳次数在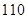以上的为优秀，试估计该校此年级跳绳成绩的优秀率是多
少？

某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60），[60,70），[70,80），[80,90），[90,100]．

（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；
（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如下表所示，
求数学成绩在[50,90）之外的人数．

分数段	[50,60）	[60, 70）	[70,80）	[80,90）
x∶y	1∶1	2∶1	3∶4	4∶5

 

某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段：，，…， 后得到如下频率分布直方图．

（Ⅰ）求分数在内的频率； 
（Ⅱ）根据频率分布直方图，估计该校高二年级学生期中考试政治成绩的平均分；
（Ⅲ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任意选取2人，求其中恰有1人的分数．不低于90分的概率．

酒后违法驾驶机动车的行为分成两个档次：“酒后驾车”和“醉酒驾车”，其检测标准是驾驶人员血液中的酒精含量（简称血酒含量，单位是毫克/100毫升），当时，为酒后驾车；当时，为醉酒驾车．某市公安局交通管理部门在某路段的一次拦查行动中，依法检查了200辆机动车驾驶员的血酒含量（如下表）．

依据上述材料回答下列问题：
（1）分别写出酒后违法驾车发生的频率和酒后违法驾车中醉酒驾车的频率；
（2）从酒后违法驾车的司机中，抽取2人，请一一列举出所有的抽取结果，并求取到的2人中含有醉酒驾车的概率．（酒后驾车的人用大写字母如表示，醉酒驾车的人用小写字母如表示）

某校高二某班的一次数学测试成绩（满分为分）的茎叶图和频率分布直方图都受到不同程度的破坏，但可见部分如下，据此解答如下问题：

（1）求分数在的频率及全班人数；
（2）求分数在之间的频数，并计算频率分布直方图中间的矩形的高；
（3）若要从分数在 之间的试卷中任取两份分析学生失分情况，在抽取的试卷中，求至少有一份分数在之间的概率．

某班50名学生在一次百米测试中，成绩全部介于13秒与18秒之间，将测试结果按如下方式分成五组：第一组，第二组， ，第五组.下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.

（Ⅰ）若成绩大于或等于14秒且小于16秒认为良好，求该班在这次百米测试中成绩良好的人数；
（Ⅱ）设m,n表示该班某两位同学的百米测试成绩，且已知求事件“”发生的概率.

某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

（1）求直方图中的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

某城市户居民的月平均用电量（单位：度），以，，，，，，分组的频率分布直方图如图．

（1）求直方图中的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，，，的四组用户中，用分层抽样的方法抽取户居民，则月平均用电量在的用户中应抽取多少户？

某校从参加高一年级期中考试的学生中随机抽出60名学生，将其数学成绩（均为整数）分成六段[40,50)，[50,60)，．．．，[90,100]后得到如图所示的部分频率分布直方图．观察图形的信息，回答下列问题：

（1）求分数在[70,80)内的频率，并补全这个频率分布直方图，统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计本次考试的平均分；
（2）若从60名学生中随机抽取2人，抽到的学生成绩在[40,60)记0分，在[60,80)记1分，在[80,100]记2分，用表示抽取结束后的总记分，求的分布列和数学期望．

某工厂对某产品的产量与单位成本的资料分析后有如下数据：

月    份	1	2	3	4	5	6
产量x千件	2	3	4	3	4	5
单位成本y元/件	73	72	71	73	69	68

（Ⅰ）求单位成本y与月产量x之间的线性回归方程．（其中已计算得：，结果保留两位小数）
（Ⅱ）当月产量为12千件时,单位成本是多少?

为了解一大片经济林生长情况，随机测量其中的60株的底部周长（单位：Cm），将周长整理后画出的频率分布表和频率分布直方图如下：观察图形，回答下列问题：

组距	频数	频率
[	6	0．1
		0．15
	9
	18
		0．25
	3	0．05
合计

（1）补充上面的频率分布表和频率分布直方图．
（2）79．5~89．5 这一组的频数、频率分别是多少？
（3）估计这次环保知识竞赛的及格率（60cm及以上为合格

某种产品特约经销商根据以往当地的需求情况，得出如下该种产品日需求量的频率分布直方图．

（Ⅰ）求图中的值，并估计日需求量的众数；
（Ⅱ）某日，经销商购进130件该种产品，根据近期市场行情，当天每售出件能获利30元，未售出的部分，每件亏损20元．设当天的需求量为件（），纯利润为S元．
（1）将S表示为的函数；
（2）根据直方图估计当天纯利润S不少于元的概率．