高中数学误差估计解答题

为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有1000名学生参加了这次竞赛．为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成的频率分布表和频数分布条形图，解答下列问题：

（1）求频率分布表中的，值，并补全频数条形图；
（2）根据频数条形图估计该样本的中位数是多少？
（3）若成绩在65.5~85.5分的学生为三等奖，问该校获得三等奖的学生约为多少人？

为了调查某厂2000名工人生产某种产品的能力，随机抽查了位工人某天生产该产品的数量，产品数量的分组区间为，，,，,频率分布直方图如图所示．已知生产的产品数量在之间的工人有6位．

（Ⅰ）求；
（Ⅱ）工厂规定从生产低于20件产品的工人中随机的选取2位工人进行培训，则这2位工人不在同一组的概率是多少？

某校从高二年级学生中随机抽取60名学生，将其期中考试的政治成绩（均为整数）分成六段： ，，…， 后得到如下频率分布直方图．

（Ⅰ）求分数在内的频率；
（Ⅱ）用分层抽样的方法在80分以上（含80分）的学生中抽取一个容量为6的样本，将该样 本看成一个总体，从中任意选取2人， 求其中恰有1人的分数不低于90分的概率．

（本小题满分12分）
某市一次全市高中男生身高统计调查数据显示：全市100 000名男生的身高服从正态分布N(168，16).现从某学校高三年级男生中随机抽取50名测量身高，测量发现被测学生身高全部介于160 cm和184 cm之间，将测量结果按如下方式分成6组：第一组 [160，164]，第二组[164，168]，…，第6组[180，184]，下图是按上述分组方法得到的频率分布直方图．

（Ⅰ）试评估该校高三年级男生在全市高中男生中的平均身高状况；
（Ⅱ）求这50名男生身高在172 cm以上（含172 cm）的人数；
（Ⅲ）在这50名男生身高在172 cm以上（含172 cm）的人中任意抽取2人，该2人中身高排名（从高到低）在全市前130名的人数记为，求的数学期望．
参考数据：
若．则
=0.6826，
="0.9544,"
=0.9974.

（本小题满分12分）
第8届中学生模拟联合国大会将在本校举行，为了搞好接待工作，组委会招募了12名男志愿者和18名女志愿者．将这30名志愿者的身高编成如下茎叶图（单位：cm）：
                       男             女
                               15    7  7  8  9  9  9
9  8   16    0  0  1  2  4  5  8  9
8  6  5  0   17    2  5  6
7  4  2  1   18    0 
1  0   19
若男生身高在180cm以上（包括180cm）定义为“高个子”， 在180cm以下（不包括180cm）定义为“非高个子”， 女生身高在170cm以上（包括170cm）定义为“高个子”，在170cm以下（不包括170cm）定义为“非高个子”．
（1）如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人，则应分别抽取“高个子”、“非高个子”各几人？
（2）从（1）中抽出的6人中选2人担任领座员，那么至少有一人是“高个子”的概率是多少？

（本小题满分12分）某校从参加高一年级期末考试的学生中抽出60名学生，将其某科成绩（是不小于40不大于100的整数）分成六段，…后画出如下频率分布直方图,根据图形中所给的信息，回答以下问题：

（1）求第四小组的频率.
（2）求样本的众数.
(3) 观察频率分布直方图图形的信息，估计这次考试的及格率（60分及以上为及格）和平均分．

某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图所示,其中 120～130(包括120分但不包括130分)的频率为0.05,此分数段的人数为5人.

(1) 问各班被抽取的学生人数各为多少人?
(2) 在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.

（本小题满分12分）
2012年3月2日，国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5（PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称可入肺颗粒物）年平均浓度不得超过35微克/立方米，PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据，数据统计如下：

组别	PM2.5（微克/立方米）	频数（天）	频率
第一组	(0,15]	4	0.1
第二组	(15,30]	12	0.3
第三组	(30,45]	8	0.2
第四组	(45,60]	8	0.2
第三组	(60,75]	4	0.1
第四组	(75,90)	4	0.1

（1）写出该样本的众数和中位数（不必写出计算过程）；
（2）求该样本的平均数，并根据样本估计总体的思想，从PM2.5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由；
（3）将频率视为概率，对于去年的某2天，记这2天中该居民区PM2.5的24小时平均浓度符合环境空气质量标准的天数为，求的分布列及数学期望．

(本小题满分12分)在育民中学举行的电脑知识竞赛中，将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组，绘制如图所示的频率分布直方图．已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30，0.15，0.10,0.05，第二小组的频数是40.

(1)求第二小组的频率，并补全这个频率分布直方图；
(2)求这两个班参赛的学生人数是多少？
(3)求两个班参赛学生的成绩的中位数。

(本题满分12分） 为了了解某中学学生的体能情况，体育组决定抽样三个年级部分学生进行跳绳测试，并将所得的数据整理后画出频率分布直方图（如图5）.已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数是5.

(1) 求第四小组的频率和参加这次测试的学生人数；
(2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？
(3) 参加这次测试跳绳次数在100次以上为优秀，试估计该校此年级跳绳成绩的优秀率是多少？

（本小题满分13分）
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图(如图)，图中从左到右各小长方形面积之比为2：4：17：15：9：3，第二小组频数为12.

(Ⅰ)第二小组的频率是多少？样本容量是多少？
(Ⅱ)若次数在110以上（含110次）为达标，试估计该学校全体高一学生的达标率是多少？（Ⅲ）在这次测试中，学生跳绳次数的中位数、众数各是是多少？（精确到0.1）

为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8:00—10:00间各自的点击量，如图所示茎叶图，根据茎叶图问：

（1）甲、乙两个网站点击量的极差分别是多少？
（2）甲网站点击量在间的频率是多少？
（3）甲、乙两个网站哪个更受欢迎？并说明理由。

如图，从参加环保知识竞赛的学生中抽出名，将其成绩（均为整数）整理后画出的频率分布直方图如下：观察图形，回答下列问题：

（1）79.5到89.5这一组的频数、频率分别是多少？
（2）估计这次环保知识竞赛的及格率（分及以上为及格）.

甲乙两个学校高三年级分别为1100人，1000人，为了统计两个学校在地区二模考试的数学科目成绩，釆用分层抽样抽取了 105名学生的成绩，并作出了部分频率分布表如下：（规定考试成绩在[120，150]内为优秀）
甲校.

分组	[70,80)	[80,90)	[90,100)	[100,110)	[110,120)	[120,130)	[130,140)	[140,150]
频数	2	3	10	15	15	X	3	1

乙校：

分组	[70,80)	[80,90)	[90,100)	[100,110]	[110,120)	[120,130)	[130,140)	[140,150]
频数	1	2	9	8	10	10	y	3

（1）计算x, y的值；
（2）由以上统计数据填写下面2X2列联表，并判断是否有97.5%的把握认为两个学校的数学成绩有差异.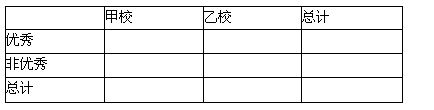

附：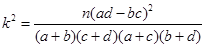

P(k2>k0)	0. 10	0. 025	0. 010
K	2. 706	5. 024	6. 635

 

为了某班学生喜爱打篮球是否与性别有关,对本班50人进行问卷调查得到了如下的列联表:

已知在全部50人中随机抽取1人,抽到不爱打篮球的学生的概率为.
(1)请将上面的列联表补充完整;
(2)是否有把握在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关;请说明理由.
附参考公式:

P()	0.05	0.025	0.010	0.005	0.001
k	3.841	5.024	6.635	7.879	10.828