(本题满分12分） 为了了解某中学学生的体能情况，体育组决定抽样三个年级部分学生进行跳绳测试，并将所得的数据整理后画出频率分布直方图（如图5）.已知图中从左到右的前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数是5.
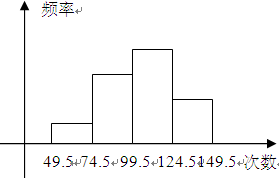
(1) 求第四小组的频率和参加这次测试的学生人数；
(2) 在这次测试中，学生跳绳次数的中位数落在第几小组内？
(3) 参加这次测试跳绳次数在100次以上为优秀，试估计该校此年级跳绳成绩的优秀率是多少？
相关试题
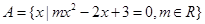，若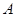
中元素至多只有一个，求
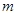的取值范围.
.
为何实数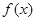
总是为增函数；
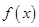的顶点坐标为
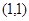，且
，
∈
，
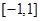的图象恒在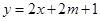
的图象上方，
的取值范围，
上单调，求实数
的取值范围.
是定义在
上的增函数，且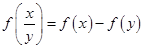
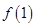的值；（2）解不等式：
；
，解不等式
,求函数
最大值和最小值;
有两根
，试求
的值.相关知识点
推荐套卷
粤公网安备 44130202000953号