[安徽]2011-2012学年安徽毫州高一下学期期末考试数学试卷
甲校有3 600名学生,乙校有5 400名学生,丙校有1 800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个容量为90人的样本,应在这三校分别抽取学生( )
| A.30人,30人,30人 | B.30人,45人,15人 |
| C.20人,30人,10人 | D.30人,50人,10人 |
200辆汽车通过某一段公路时,时速的频率分布直方图如右图所示,则时速在[50,70)的汽车大约有( )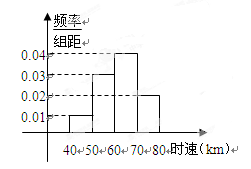
| A.60辆 | B.80辆 | C.70辆 | D.140辆 |
要得到函数y=sin(2x-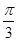 )的图象,应该把函数y=sin2x的图象( )
)的图象,应该把函数y=sin2x的图象( )
A.向左平移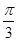 |
B.向右平移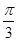 |
C.向左平移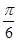 |
D.向右平移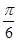 |
班级需要在甲、乙、丙三位同学中随机的抽取两位参加一项活动,则正好抽到的是甲乙的概率是( )
A.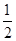 |
B.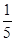 |
C.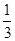 |
D.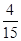 |
若函数f(x)=2sin(ωx+φ)的部分图像如图所示,则ω和φ的取值是( )
A.ω=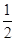 ,φ=- ,φ=-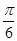 |
B.ω=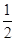 ,φ= ,φ=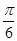 |
C.ω=1,φ=-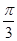 |
D.ω=1,φ=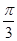 |
已知a=(cosα,sinα),b=(cosβ,sinβ),则( )
| A.a⊥b | B.a∥b | C.(a+b)⊥(a-b) | D.a与b的夹角为α+β |
已知|a|=3,| b |=4,(a+b)×( a+3 b)=33,则a与b的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
一个容量为20的样本数据,分组后,组距与频数如下: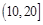 ,2;
,2; , 3;
, 3; 4;
4;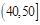 ,5;
,5; 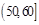 ,4 ;
,4 ;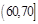 ,2。则样本在区间
,2。则样本在区间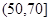 上的频率为__________;
上的频率为__________;
一般情况下,年龄在18至38岁的人们,其体重y(kg)对身高x(cm)的回归方程为y=0.7x-52,李明同学身高为180cm,那么他的体重估计为 ___ kg.
若角α的终边落在直线x+y=0上,则+的值等于__________;,则+的值等于__________;
下列五个命题:
①函数y=tan(-)的对称中心是(2kπ+,0)(k∈Z).
②终边在y轴上的角的集合是{α|α=,k∈Z}.
③在同一坐标系中,函数y=sinx的图像和函数y=x的图像有三个公共点.
④把函数y=3sin(2x+)的图像向右平移得到y=3sin2x的图像.
⑤函数y=sin(x-)在[0,π]上是减少的.
其中,正确命题的序号是__________.(写出所有正确命题的序号)
学校为了对某课题进行研究,用分层抽样方法从三个年级高一、高二、高三的相关老师中,抽取若干人组成研究小组,有关数据见下表(单位:人).
| 年级 |
相关人数 |
抽取人数 |
| 高一 |
18 |
x |
| 高二 |
36 |
2 |
| 高三 |
54 |
y |
(1)求x,y;
(2)若从高二、高三抽取的人中选2人做专题发言,求这2人都来自高三的概率。
下图是总体的一样本频率分布直方图,且在[15,18)内频数为8.
(1)求样本容量;
(2)若在[12,15)内小矩形面积为0.06,求在[12,15)内频数;
(3)在(2)的条件下,求样本在[18,33)内的频率.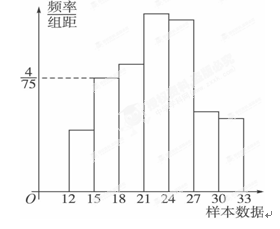
已知坐标平面内两点A=(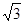 ,-1), B=(
,-1), B=(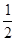 ,
, 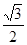 ),O为原点。
),O为原点。
(1)证明OA⊥OB;
(2)设a =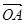 ,b=
,b=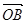 ,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
,若存在不同时为零的实数k、t,使得x=a+(t2-3)b,y=-ka+tb,且x⊥y,求函数关系式k=f(t).
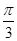
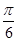
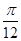
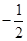
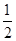
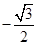
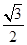
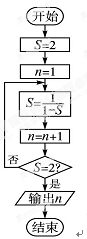
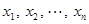 的平均数是10,则对于样本数据
的平均数是10,则对于样本数据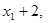
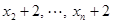 ,平均数为 ____________;
,平均数为 ____________;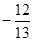 ,cos(α+β)=
,cos(α+β)=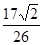 ,且α∈(π,
,且α∈(π,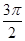 ),α+β∈(
),α+β∈(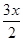 ,sin
,sin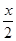 ,-sin
,-sin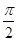 ],
], 粤公网安备 44130202000953号
粤公网安备 44130202000953号