某校从参加高三年级理科综合物理考试的学生中随机抽出 名学生,将其数学成绩(均为整数)分成六段
名学生,将其数学成绩(均为整数)分成六段 ,
, …
… 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求分数在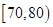 内的频率,并补全这个频率分布直方图;
内的频率,并补全这个频率分布直方图;
(Ⅱ)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试的
平均分;
(Ⅲ)若从 名学生中随机抽取
名学生中随机抽取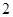 人,抽到的学生成绩在
人,抽到的学生成绩在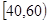 记
记 分,在
分,在 记
记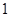 分,
分,
在 记
记 分,用
分,用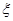 表示抽取结束后的总记分,求
表示抽取结束后的总记分,求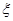 的分布列和数学期望.
的分布列和数学期望.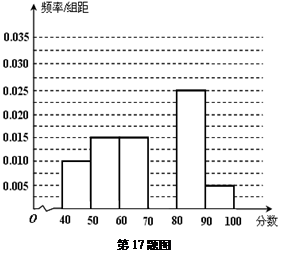
相关知识点
推荐套卷
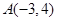 点射出,到
点射出,到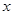 轴上的
轴上的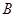 点后,被
点后,被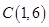 ,求
,求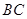 所在直线的方程及点
所在直线的方程及点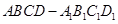 的棱长为
的棱长为 ,线段
,线段 上有两个动点
上有两个动点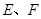 ,且
,且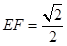 ,则下列结论中错误的是( )
,则下列结论中错误的是( )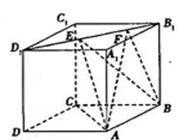

 的体积为定值
的体积为定值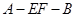 的大小为定值
的大小为定值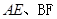 所成角为定值
所成角为定值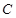 :
: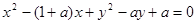 .
.
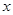 轴相切,求圆
轴相切,求圆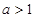 ,圆C与
,圆C与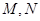 (点
(点 在点
在点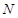 的左侧).过点
的左侧).过点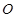 :
: 相交于两点
相交于两点 .问:是否存在实数
.问:是否存在实数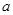 ,使得
,使得 ?若存在,求出实数
?若存在,求出实数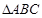 与
与 所在平面互相垂直,且
所在平面互相垂直,且 ,
,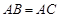 ,
, ,点
,点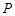 ,
,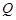 分别在线段
分别在线段 上,沿直线
上,沿直线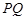 将
将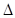
 向上翻折,使
向上翻折,使 与
与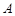 重合.
重合.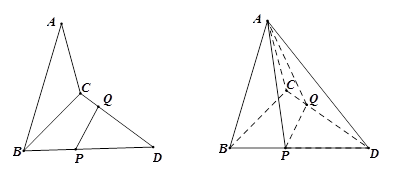
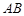
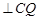 ;
;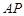 与平面
与平面 所成的角的正弦值.
所成的角的正弦值.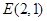 和圆
和圆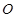 :
: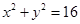 .
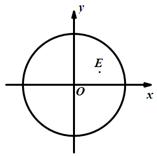
.
 的直线
的直线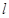 被圆
被圆 ,求直线
,求直线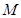 :
: ?若存在,求出点
?若存在,求出点 粤公网安备 44130202000953号
粤公网安备 44130202000953号