[福建]2012届福建省漳州市四地七校高三第四次联考理科数学试卷
已知i是虚数单位,复数z=i2(1+i)的虚部为( )
| A.-i | B. i | C.-1 | D. 1 |
设 或
或 ,
, 或
或 ,则
,则 是
是 的 ( )
的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设 、
、 是两个不同的平面,
是两个不同的平面, 、
、 是两条不同的直线,给出下列4个命题,其中正确命题是( )
是两条不同的直线,给出下列4个命题,其中正确命题是( )
A.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
C.若 ⊥ ⊥ , , ⊥ ⊥ , , ⊥ ⊥ ,则 ,则 ⊥ ⊥ |
D.若 、 、 在平面 在平面 内的射影互相垂直,则 内的射影互相垂直,则 ⊥ ⊥ |
如图,用4种不同的颜色对图中5个区域涂色(4种颜色全部使用),要求每个区域涂一种颜色,相邻的区域不能涂相同的颜色,则不同的涂色种数有( )
| A.72种 | B.96种 | C.108种 | D.120种 |
设椭圆以正方形的两个顶点为焦点且过另外两个顶点,那么此椭圆的离心率为( )
A. |
B. |
C. |
D. 或 或 |
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是( )
| A.36 cm3 | B.48 cm3 | C.60 cm3 | D.72 cm3 |
下边方框中是一个求20个数的平均数的程序,则在横线上可填的语句为( )
A. |
B. |
C. |
D. |
设a,b,m为正整数,若a和b除以m的余数相同,则称a和b对m同余. 记作 ,已知
,已知 ,则b的值可以是 ( )
,则b的值可以是 ( )
| A.1012 | B.2009 | C.3003 | D.6001 |
从双曲线 的左焦点
的左焦点 引圆
引圆 的切线,切点为T,延长FT交双曲线右支于点P,O为坐标原点,M为PF 的中点,则
的切线,切点为T,延长FT交双曲线右支于点P,O为坐标原点,M为PF 的中点,则  与
与 的大小关系为( ) .
的大小关系为( ) .
A. |
B. |
C. |
D.不能确定 |
已知函数 的最大值为3,
的最大值为3, 的图像与
的图像与 轴的交点坐标为
轴的交点坐标为 ,其相邻两条对称轴间的距离为
,其相邻两条对称轴间的距离为 ,则
,则
 ____________.
____________.
下图展示了一个由区间(0,1)到实数集R的映射过程:区间 中的实数m对应数轴上的点M,如图1;将线段
中的实数m对应数轴上的点M,如图1;将线段 围成一个圆,使两端点A、B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图2;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为 ,如图3.图3中直线
,如图3.图3中直线 与x轴交于点
与x轴交于点 ,则m的象就是n,记作
,则m的象就是n,记作 .
.


下列说法中正确命题的序号是 .(填出所有正确命题的序号)
④  ;②
;② 是奇函数; ③
是奇函数; ③ 在定义域上单调函数;
在定义域上单调函数;
④ 的图象关于点
的图象关于点 对称.
对称.
(本小题满分13分)已知函数 ,将函数
,将函数 的所有极值点从小到大排成一数列,记为
的所有极值点从小到大排成一数列,记为
(1)求数列 的通项公式;
的通项公式;
(2)令 ,求数列
,求数列 前n项和
前n项和
如图,在三棱柱 中,已知
中,已知

 侧面
侧面

(Ⅰ)求直线C1B与底面ABC所成角正切值;
(Ⅱ)在棱 (不包含端点
(不包含端点 上确定一点
上确定一点 的位置,使得
的位置,使得 (要求说明理由).
(要求说明理由).
(Ⅲ)在(2)的条件下,若 ,求二面角
,求二面角 的大小.
的大小.
(本小题满分13分)对某校高一年级的学生参加社区服务的次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了下图所示的频数与频率的统计表和频率分布直方图:
(I)求出表中M、p及图中a的值
(II)学校决定对参加社区服务的学生进行表彰,对参加活动次数在[25,30]区间的每个学生发放价值80元的学习用品,对参加活动次数在[20,25)区间的每个学生发放价值60元的学习用品,对参加活动次数在[15,20)区间的每个学生发放价值40元的学习用品,对参加活动次数在[10,15)区间的每个学生发放价值20元的学习用品,在所抽取的这M名学生中,任意取出2人,设X为此二人所获得学习用品价值之差的绝对值,求X的分布列与数学期望E(X)。
(本小题满分13分)已知两点 ,
, ,曲线
,曲线 上的动点
上的动点 满足
满足 ,直线
,直线 与曲线
与曲线 交于另一点
交于另一点 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设 ,若
,若
 ,求直线
,求直线 的方程.
的方程.
(本小题满分14分)已知函数 同时满足如下三个条件:①定义域为
同时满足如下三个条件:①定义域为 ;②
;② 是偶函数;③
是偶函数;③ 时,
时, ,其中
,其中 .
.
(Ⅰ)求 在
在 上的解析式,并求出函数
上的解析式,并求出函数 的最大值;
的最大值;
(Ⅱ)当 ,
, 时,函数
时,函数 ,若
,若 的图象恒在直线
的图象恒在直线 上方,求实数
上方,求实数 的取值范围(其中
的取值范围(其中 为自然对数的底数,
为自然对数的底数, ).
).
(选修4—2 矩阵与变换)
变换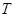 是将平面上每个点
是将平面上每个点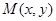 的横坐标乘2,纵坐标乘4,变到点
的横坐标乘2,纵坐标乘4,变到点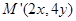 。
。
(Ⅰ)求变换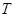 的矩阵;
的矩阵;
(Ⅱ)圆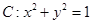 在变换
在变换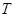 的作用下变成了什么图形?
的作用下变成了什么图形?
(选修4—4 参数方程与极坐标)
在极坐标系下,已知圆O: 和直线
和直线 ,
,
(Ⅰ)求圆O和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)当 时,求直线
时,求直线 与圆O公共点的一个极坐标.
与圆O公共点的一个极坐标.

 被圆
被圆 所截得的弦长为
所截得的弦长为 ,则
,则 的最小值为( )
的最小值为( )


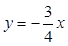 上,则
上,则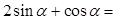 _________.
_________. ,直线
,直线 ,直线
,直线 围成的封闭图形的面积为_________.
围成的封闭图形的面积为_________. 求得,则
求得,则 .
.
 和
和 ,不等式
,不等式 恒成立,试求实数
恒成立,试求实数 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号