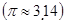如图所示,设计一个四棱锥形冷水塔塔顶,四棱锥的底面是正方形,侧面是全等的等腰三角形,已知底面边长为2m,高为 m,制造这个塔顶需要多少铁板?
m,制造这个塔顶需要多少铁板?
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
在三棱锥P-ABC中, .
.
(1)求证:平面 平面
平面 ;
;
(2)求BC与平面PAB所成角的正弦值;
(3)在棱BC上是否存在点Q使得AQ与PC成 的角?若存在,求BQ的长;若不存在,请说明理由.
的角?若存在,求BQ的长;若不存在,请说明理由.
如图,在四面体
中,
平面
,
.
是
的中点,
是
的中点,点
在线段
上,且
.
(1)证明:
平面
;
(2)若二面角
的大小为60°,求
的大小.
如图,直三棱柱 中,
中, ,
, ,
, 是
是 的中点,△
的中点,△ 是等腰三角形,
是等腰三角形, 为
为 的中点,
的中点,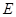 为
为 上一点.
上一点.
(1)若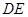 ∥平面
∥平面 ,求
,求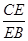 ;
;
(2)平面 将三棱柱
将三棱柱 分成两个部分,求较小部分与较大部分的体积之比.
分成两个部分,求较小部分与较大部分的体积之比.
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, .
.
(1)求证 ,并指出异面直线PA与CD所成角的大小;
,并指出异面直线PA与CD所成角的大小;
(2)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 ?如果存在,求出此时三棱锥
?如果存在,求出此时三棱锥 与四棱锥
与四棱锥 的体积比;如果不存在,请说明理由.
的体积比;如果不存在,请说明理由.
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线 AE、CF都与平面ABCD垂直,AE=1,CF=2.
AE、CF都与平面ABCD垂直,AE=1,CF=2.
(1)求二面角B-AF-D的大小;
(2)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
设倒圆锥形容器的轴截面为一个等边三角形,在此容器内注入水,并浸入半径为 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台的母线长.
在斜三棱柱 中,侧面
中,侧面 平面
平面 ,
, ,
, 为
为 中点.
中点.
(1)求证: ;
;
(2)求证: 平面
平面 ;
;
(3)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
如图所示,圆锥的轴截面为等腰直角 ,
, 为底面圆周上一点.
为底面圆周上一点.
(1)若 的中点为
的中点为 ,
, ,
,
求证: 平面
平面 ;
;
(2)如果 ,
, ,求此圆锥的全面积.
,求此圆锥的全面积.
如图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了并流入杯中,会溢出杯子吗?请用你的计算数据说明理由。(冰、水的体积差异忽略不计)