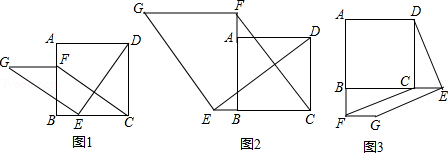
如图1,在正方形 中,点 , 分别是边 , 上的点,且 .连接 ,过点 作 ,使 ,连接 , .
(1)请判断: 与 的数量关系是 ,位置关系是 ;
(2)如图2,若点 , 分别是边 , 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点 , 分别是边 , 延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
(回顾)
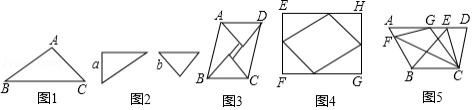
如图1, 中, , , ,则 的面积等于 .
(探究)
图2是同学们熟悉的一副三角尺,一个含有 的角,较短的直角边长为 ;另一个含有 的角,直角边长为 ,小明用两副这样的三角尺拼成一个平行四边形 (如图 ,用了两种不同的方法计算它的面积,从而推出 ,小丽用两副这样的三角尺拼成了一个矩形 (如图 ,也推出 ,请你写出小明或小丽推出 的具体说理过程.
(应用)
在四边形 中, , , , , (如图5)
(1)点 在 上,设 ,求 的最小值;
(2)点 在 上,将 沿 翻折,点 落在 上的点 处,点 是 的中点吗?说明理由.
(探索发现)
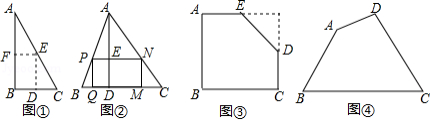
如图①,是一张直角三角形纸片, ,小明想从中剪出一个以 为内角且面积最大的矩形,经过多次操作发现,当沿着中位线 、 剪下时,所得的矩形的面积最大,随后,他通过证明验证了其正确性,并得出:矩形的最大面积与原三角形面积的比值为 .
(拓展应用)
如图②,在 中, , 边上的高 ,矩形 的顶点 、 分别在边 、 上,顶点 、 在边 上,则矩形 面积的最大值为 .(用含 , 的代数式表示)
(灵活应用)
如图③,有一块“缺角矩形” , , , , ,小明从中剪出了一个面积最大的矩形( 为所剪出矩形的内角),求该矩形的面积.
(实际应用)
如图④,现有一块四边形的木板余料 ,经测量 , , ,且 ,木匠徐师傅从这块余料中裁出了顶点 、 在边 上且面积最大的矩形 ,求该矩形的面积.
如图,已知矩形 中, , ,动点 从点 出发,在边 上以每秒1个单位的速度向点 运动,连接 ,作点 关于直线 的对称点 ,设点 的运动时间为 .
(1)若 ,求当 , , 三点在同一直线上时对应的 的值.
(2)已知 满足:在动点 从点 到点 的整个运动过程中,有且只有一个时刻 ,使点 到直线 的距离等于3,求所有这样的 的取值范围.

在平面直角坐标系中,已知 、 、 、 .
(1)四边形 的周长的最小值为 ,此时四边形 的形状为 ;
(2)在(1)的情况下, 为 的中点, 为 上一动点,连接 ,作 交四边形的边于点 ,在点 从 运动到 的过程中:
①求 的值;
②若 的中点为 ,在整个运动过程中,请直接写出点 所经过的路线长.

在平面直角坐标系中,已知 、 、 、 .
(1)四边形 的周长的最小值为 ,此时四边形 的形状为 ;
(2)在(1)的情况下, 为 的中点, 为 上一动点,连接 ,作 交四边形的边于点 ,在点 从 运动到 的过程中:
①求 的值;
②若 的中点为 ,在整个运动过程中,请直接写出点 所经过的路线长.

如图,在矩形纸片 中,已知 , ,点 在边 上移动,连接 ,将多边形 沿直线 翻折,得到多边形 ,点 、 的对应点分别为点 、 .
(1)当 恰好经过点 时(如图 ),求线段 的长;
(2)若 分别交边 , 于点 , ,且 (如图 ,求 的面积;
(3)在点 从点 移动到点 的过程中,求点 运动的路径长.

问题呈现:
如图1,点 、 、 、 分别在矩形 的边 、 、 、 上, ,求证: .( 表示面积)
实验探究:
某数学实验小组发现:若图1中 ,点 在 上移动时,上述结论会发生变化,分别过点 、 作 边的平行线,再分别过点 、 作 边的平行线,四条平行线分别相交于点 、 、 、 ,得到矩形 .
如图2,当 时,若将点 向点 靠近 ,经过探索,发现: .
如图3,当 时,若将点 向点 靠近 ,请探索 、 与 之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
(1)如图4,点 、 、 、 分别是面积为25的正方形 各边上的点,已知 , , , ,求 的长.
(2)如图5,在矩形 中, , ,点 、 分别在边 、 上, , ,点 、 分别是边 、 上的动点,且 ,连接 、 ,请直接写出四边形 面积的最大值.

如图1,在四边形 中,如果对角线 和 相交并且相等,那么我们把这样的四边形称为等角线四边形.

(1)①在“平行四边形、矩形、菱形”中, 一定是等角线四边形(填写图形名称);
②若 、 、 、 分别是等角线四边形 四边 、 、 、 的中点,当对角线 、 还要满足 时,四边形 是正方形.
(2)如图2,已知 中, , , , 为平面内一点.
①若四边形 是等角线四边形,且 ,则四边形 的面积是 ;
②设点 是以 为圆心,1为半径的圆上的动点,若四边形 是等角线四边形,写出四边形 面积的最大值,并说明理由.
已知正方形 的边长为4,一个以点 为顶点的 角绕点 旋转,角的两边分别与边 、 的延长线交于点 、 ,连接 .设 , .
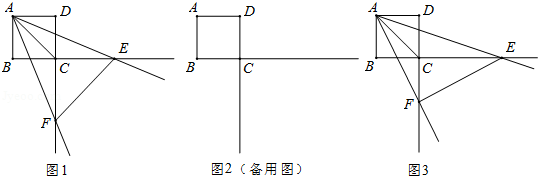
(1)如图1,当 被对角线 平分时,求 、 的值;
(2)当 是直角三角形时,求 、 的值;
(3)如图3,探索 绕点 旋转的过程中 、 满足的关系式,并说明理由.
已知正方形 , 为射线 上的一点,以 为边作正方形 ,使点 在线段 的延长线上,连接 、 .
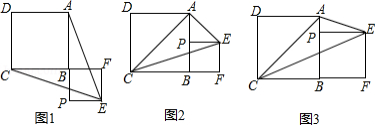
(1)如图1,若点 在线段 的延长线上,求证: ;
(2)若点 在线段 上.
①如图2,连接 ,当 为 的中点时,判断 的形状,并说明理由;
②如图3,设 , ,当 平分 时,求 及 的度数.
(1)阅读材料:
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线 剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板 ,沿中位线 剪掉 ,请把纸板剩下的部分 剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
如图3,把一边长为 的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中 ,延长 、 分别与 、 交于点 、 ,点 、 分别为 、 的中点,在线段 和 处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)

如图,四边形 是菱形, ,点 在射线 上(不包括点 和点 ,过点 的直线 交直线 于点 ,交直线 于点 ,且 ,点 在 的延长线上, ,连接 , , .
(1)如图1,当点 在线段 上时,
①判断 的形状,并说明理由.
②求证: 是等边三角形.
(2)如图2,当点 在 的延长线上时, 是等边三角形吗?如果是,请证明你的结论;如果不是,请说明理由.

如图,点 是正方形 的对角线 延长线上的一点,连接 ,过点 作 交 的延长线于点 ,过点 作 于点 ,则下列结论中:
① ;② ;③ ;④
正确的是 (填写所有正确结论的序号)
