如图,点 , 分别在正方形 的边 , 上,且 ,点 在射线 上(点 不与点 重合).将线段 绕点 顺时针旋转 得到线段 ,过点 作 的垂线 ,垂足为点 ,交射线 于点 .
(1)如图1,若点 是 的中点,点 在线段 上,线段 , , 的数量关系为 .
(2)如图2,若点 不是 的中点,点 在线段 上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由.
(3)正方形 的边长为6, , ,请直接写出线段 的长.

相关知识点
推荐套卷
 .
.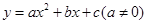 的图象如图所示,根据图象解答下列问题:
的图象如图所示,根据图象解答下列问题: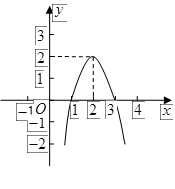
 的两个根;
的两个根;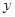 随
随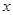 的增大而减小的自变量
的增大而减小的自变量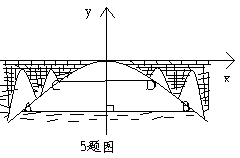
 粤公网安备 44130202000953号
粤公网安备 44130202000953号