如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

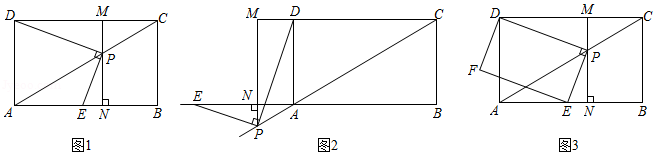
如图1,在正方形ABCD内作∠EAF=45°,AE交BC于点E,AF交CD于点F,连接EF,过点A作AH⊥EF,垂足为H.
(1)如图2,将△ADF绕点A顺时针旋转90°得到△ABG.
①求证:△AGE≌△AFE;
②若BE=2,DF=3,求AH的长.
(2)如图3,连接BD交AE于点M,交AF于点N.请探究并猜想:线段BM,MN,ND之间有什么数量关系?并说明理由.

如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知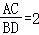 ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

如图,已知正方形ABCD边长为1,∠EAF=45°,AE=AF,则有下列结论:
①∠1=∠2=22.5°;
②点C到EF的距离是 ;
③△ECF的周长为2;
④BE+DF>EF.
其中正确的结论是 .(写出所有正确结论的序号)

如图,矩形  的对角线
的对角线  ,
,  相交于点
相交于点  ,
,  关于
关于  的对称图形为
的对称图形为  .
.
(1)求证:四边形  是菱形;
是菱形;
(2)连接  ,若
,若  ,
,  .
.
①求  的值;
的值;
②若点  为线段
为线段  上一动点(不与点
上一动点(不与点  重合),连接
重合),连接  ,一动点
,一动点  从点
从点  出发,以
出发,以  的速度沿线段
的速度沿线段  匀速运动到点
匀速运动到点  ,再以
,再以  的速度沿线段
的速度沿线段  匀速运动到点
匀速运动到点  ,到达点
,到达点  后停止运动,当点
后停止运动,当点  沿上述路线运动到点
沿上述路线运动到点  所需要的时间最短时,求
所需要的时间最短时,求  的长和点
的长和点  走完全程所需的时间.
走完全程所需的时间.

如图,平面直角坐标系中  是原点,
是原点,  的顶点
的顶点  ,
,  的坐标分别是
的坐标分别是  ,
,  ,点
,点  ,
,  把线段
把线段  三等分,延长
三等分,延长  、
、  分别交
分别交  、
、  于点
于点  ,
,  ,连接
,连接  .则下列结论:
.则下列结论:
①  是
是  的中点;②
的中点;②  与
与  相似;③四边形
相似;③四边形  的面积是
;④
的面积是
;④
其中正确的结论是 (填写所有正确结论的序号).

如图, BD是正方形 ABCD的对角线, BC=2,边 BC在其所在的直线上平移,将通过平移得到的线段记为 PQ,连接 PA、 QD,并过点 Q作 QO⊥ BD,垂足为 O,连接 OA、 OP.
(1)请直接写出线段 BC在平移过程中,四边形 APQD是什么四边形?
(2)请判断 OA、 OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设 y= S △ OPB, BP= x(0≤ x≤2),求 y与 x之间的函数关系式,并求出 y的最大值.

如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.
中心为 的正六边形 的半径为 ,点 , 同时分别从 , 两点出发,以 的速度沿 , 向终点 , 运动,连接 , , , ,设运动时间为 .
(1)求证:四边形 为平行四边形;
(2)求矩形 的面积与正六边形 的面积之比.

如图,矩形 中,点 为对角线 所在直线上的一个动点,连接 ,过点 作 ,交直线 于点 ,过点 作 ,交直线 于点 ,交直线 于点 . , .
(1)如图1,①当点 在线段 上时, 和 的数量关系为: ;
② 的值是 ;
(2)如图2,当点 在 延长线上时,(1)中的结论②是否成立?若成立,请证明;若不成立,说明理由;
(3)如图3,以线段 , 为邻边作矩形 .设 的长为 ,矩形 的面积为 .请直接写出 与 之间的函数关系式及 的最小值.

如图,四边形 是正方形,点 是射线 上的动点,连接 ,以 为对角线作正方形 , , , 按逆时针排列),连接 , .
(1)当点 在线段 上时.
①求证: ;
②求证: ;
(2)设正方形 的面积为 ,正方形 的面积为 ,以 , , , 为顶点的四边形的面积为 ,当 时,请直接写出 的值.

如图,正方形 和正方形 (其中 , 的延长线与直线 交于点 .
(1)如图1,当点 在 上时,求证: , ;
(2)将正方形 绕点 旋转一周.
①如图2,当点 在直线 右侧时,求证: ;
②当 时,若 , ,请直接写出线段 的长.

如图,在 中, , , 是 边上的一点,连接 ,作 于点 ,过点 作 的垂线交 的延长线于点 .
(1)如图1,求证: ;
(2)如图2,以 , 为邻边作平行四边形 ,连接 交 于点 ,连接 ,求 的值;
(3)如图3,若 是 的中点,以 , 为邻边作平行四边形 ,连接 交 于点 ,连接 ,经探究发现 ,请直接写出 的值.

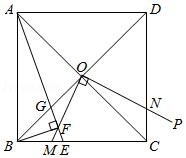
如图,在正方形 中,对角线 , 相交于点 ,点 在 边上,且 ,连接 交 于点 ,过点 作 于点 ,连接 并延长,交 于点 ,过点 作 交 于点 , ,现给出下列结论:① ;② ;③ ;④ ;其中正确的结论有
| A. |
①②③ |
B. |
②③④ |
C. |
①②④ |
D. |
①③④ |