在矩形 中，点 是射线 上一动点，连接 ，过点 作 于点 ，交直线 于点 ．
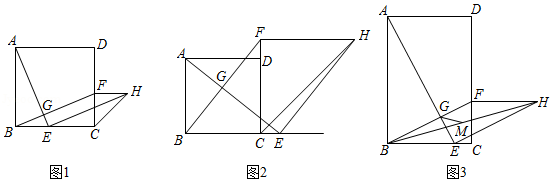
（1）当矩形 是正方形时，以点 为直角顶点在正方形 的外部作等腰直角三角形 ，连接 ．
①如图1，若点 在线段 上，则线段 与 之间的数量关系是 ，位置关系是 ；
②如图2，若点 在线段 的延长线上，①中的结论还成立吗？如果成立，请给予证明；如果不成立，请说明理由；
（2）如图3，若点 在线段 上，以 和 为邻边作平行四边形 ， 是 中点，连接 ， ， ，求 的最小值．
相关试题
，其中
。
；(2)
；
； （4）
小明的妈妈在菜市场买回3斤萝卜、2斤排骨，准备做萝卜排骨汤。
妈妈：“今天买这两样菜共花了45元，上月买同样重量的这两种菜只要36元”；
爸爸：“报纸上说了萝卜的单价上涨了50％，排骨的单价上涨了20％”；
小明：“爸爸、妈妈，我想知道今天买的萝卜和排骨的单价分别是多少?”
请你根据上述信息，通过列方程组替小明求解这天萝卜、排骨的单价（单位：元／斤）。
相关知识点
推荐套卷
粤公网安备 44130202000953号