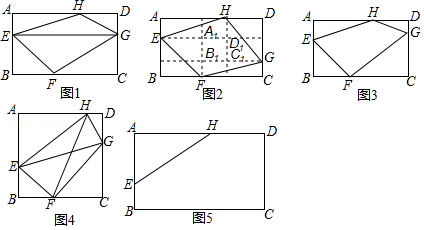
问题呈现:
如图1,点 、 、 、 分别在矩形 的边 、 、 、 上, ,求证: .( 表示面积)
实验探究:
某数学实验小组发现:若图1中 ,点 在 上移动时,上述结论会发生变化,分别过点 、 作 边的平行线,再分别过点 、 作 边的平行线,四条平行线分别相交于点 、 、 、 ,得到矩形 .
如图2,当 时,若将点 向点 靠近 ,经过探索,发现: .
如图3,当 时,若将点 向点 靠近 ,请探索 、 与 之间的数量关系,并说明理由.
迁移应用:
请直接应用“实验探究”中发现的结论解答下列问题:
(1)如图4,点 、 、 、 分别是面积为25的正方形 各边上的点,已知 , , , ,求 的长.
(2)如图5,在矩形 中, , ,点 、 分别在边 、 上, , ,点 、 分别是边 、 上的动点,且 ,连接 、 ,请直接写出四边形 面积的最大值.
推荐套卷
 粤公网安备 44130202000953号
粤公网安备 44130202000953号