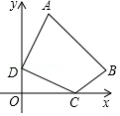
在平面直角坐标系中，已知 、 、 、 ．
（1）四边形 的周长的最小值为 ，此时四边形 的形状为 ；
（2）在（1）的情况下， 为 的中点， 为 上一动点，连接 ，作 交四边形的边于点 ，在点 从 运动到 的过程中：
①求 的值；
②若 的中点为 ，在整个运动过程中，请直接写出点 所经过的路线长．
；⑷81(a＋b)2－16(a－b)2．
)－2－(π－1)0－|－3|；⑵（－2p－q）（－q＋2p）；
的值．
，其中x是方程
的根.相关知识点
推荐套卷
在平面直角坐标系中，已知 、 、 、 ．
（1）四边形 的周长的最小值为 ，此时四边形 的形状为 ；
（2）在（1）的情况下， 为 的中点， 为 上一动点，连接 ，作 交四边形的边于点 ，在点 从 运动到 的过程中：
①求 的值；
②若 的中点为 ，在整个运动过程中，请直接写出点 所经过的路线长．
粤公网安备 44130202000953号