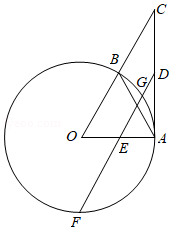
如图, , 是 上两点,且 ,连接 并延长到点 ,使 ,连接 .
(1)求证: 是 的切线;
(2)点 , 分别是 , 的中点, 所在直线交 于点 , , ,求 的长.
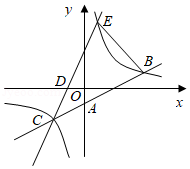
如图,反比例函数的图象与过点 , 的直线交于点 和 .
(1)求直线 和反比例函数的解析式;
(2)已知点 ,直线 与反比例函数图象在第一象限的交点为 ,直接写出点 的坐标,并求 的面积.
已知关于 的一元二次方程 .
(1)求证:无论 取何值,方程都有两个不相等的实数根.
(2)如果方程的两个实数根为 , ,且 与 都为整数,求 所有可能的值.
某市体育中考自选项目有乒乓球、篮球和羽毛球,每个考生任选一项作为自选考试项目.
(1)求考生小红和小强自选项目相同的概率;
(2)除自选项目之外,长跑和掷实心球为必考项目.小红和小强的体育中考各项成绩(百分制)的统计图表如下:

考生 |
自选项目 |
长跑 |
掷实心球 |
小红 |
95 |
90 |
95 |
小强 |
90 |
95 |
95 |
①补全条形统计图.
②如果体育中考按自选项目占 、长跑占 、掷实心球占 计算成绩(百分制),分别计算小红和小强的体育中考成绩.
如图, , 是海面上位于东西方向的两个观测点,有一艘海轮在 点处遇险发出求救信号,此时测得 点位于观测点 的北偏东 方向上,同时位于观测点 的北偏西 方向上,且测得 点与观测点 的距离为 海里.
(1)求观测点 与 点之间的距离;
(2)有一艘救援船位于观测点 的正南方向且与观测点 相距30海里的 点处,在接到海轮的求救信号后立即前往营救,其航行速度为42海里 小时,求救援船到达 点需要的最少时间.

一次函数 的图象与反比例函数 的图象相交于 , 两点.
(1)求一次函数的解析式;
(2)将直线 沿 轴向下平移8个单位后得到直线 , 与两坐标轴分别相交于 , ,与反比例函数的图象相交于点 , ,求 的值.
某运输公司有 、 两种货车,3辆 货车与2辆 货车一次可以运货90吨,5辆 货车与4辆 货车一次可以运货160吨.
(1)请问1辆 货车和1辆 货车一次可以分别运货多少吨?
(2)目前有190吨货物需要运输,该运输公司计划安排 、 两种货车将全部货物一次运完 、 两种货车均满载),其中每辆 货车一次运货花费500元,每辆 货车一次运货花费400元.请你列出所有的运输方案,并指出哪种运输方案费用最少.
某合作社为帮助农民增收致富,根据网络平台销售当地的一种农副产品.为了解该农副产品在一个季度内每天的销售额,从中随机抽取了20天的销售额(单位:万元)作为样本,数据如下:
16 14 13 17 15 14 16 17 14 14
15 14 15 15 14 16 12 13 13 16
(1)根据上述样本数据,补全条形统计图;
(2)上述样本数据的众数是 ,中位数是 ;
(3)根据样本数据,估计这种农副产品在该季度内平均每天的销售额.

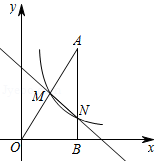
如图, 中, ,边 在 轴上,反比例函数 的图象经过斜边 的中点 ,与 相交于点 , , .
(1)求 的值;
(2)求直线 的解析式.
阅读以下材料:
苏格兰数学家纳皮尔 . , 年)是对数的创始人.他发明对数是在指数书写方式之前,直到18世纪瑞士数学家欧拉 , 年)才发现指数与对数之间的联系.
对数的定义:一般地,若 且 ,那么 叫做以 为底 的对数,记作 ,比如指数式 可以转化为对数式 ,对数式 可以转化为指数式 .
我们根据对数的定义可得到对数的一个性质:
, , , ,理由如下:
设 , ,则 , ,
,由对数的定义得 .
又 ,
.
根据上述材料,结合你所学的知识,解答下列问题:
(1)填空:① ,② ,③ ;
(2)求证: , , , ;
(3)拓展运用:计算 .