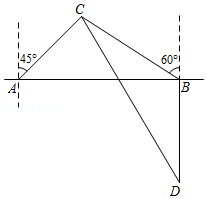
如图， ， 是海面上位于东西方向的两个观测点，有一艘海轮在 点处遇险发出求救信号，此时测得 点位于观测点 的北偏东 方向上，同时位于观测点 的北偏西 方向上，且测得 点与观测点 的距离为 海里．
（1）求观测点 与 点之间的距离；
（2）有一艘救援船位于观测点 的正南方向且与观测点 相距30海里的 点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里 小时，求救援船到达 点需要的最少时间．
相关试题
甲、乙两班参加植树活
动．乙班先植树30棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为
（棵），乙班植树的总量为
（棵），两班一起植树所用的时间（从甲班开始植树时计时）为
（时），、分别与之间的部分函数图象如图9
所示．
（1）当0≤x≤6时，分别求、与之间的函数关系式；
（2）如果甲、乙两班均保持前6个小时的工作效率，通过计算说明，当
时，甲、乙两班植树的总量之和能否超过
棵．
如图8，在△ABC中，D，E在直线BC上．
（1）若AB=BC=AC=CE=BD，求∠EAC的度数；
（2）若AB=AC=CE=BD，∠DAE=100°，求∠EAC的度数．
如图7，在边长为a的正方形纸片的四个角都剪去一个长为m、宽为n的矩形．
（1）用含a，m，n的式子表示纸片剩余部分的面积；
（2）当m=3，n=5，且剩余部分的面积等于229时，求正方形的边长a的值
,其中
C上，AF=DE，BE="CF." 求证：∠A=∠D．
相关知识点
推荐套卷
粤公网安备 44130202000953号