如图,为测量建筑物 的高度,在 点测得建筑物顶部 点的仰角为 ,再向建筑物 前进30米到达 点,测得建筑物顶部 点的仰角为 , , 三点在一条直线上),求建筑物 的高度.(结果保留整数.参考数据: , , , , ,

如图所示,某建筑物楼顶有信号塔 ,卓玛同学为了探究信号塔 的高度,从建筑物一层 点沿直线 出发,到达 点时刚好能看到信号塔的最高点 ,测得仰角 , 长7米.接着卓玛再从 点出发,继续沿 方向走了8米后到达 点,此时刚好能看到信号塔的最低点 ,测得仰角 .(不计卓玛同学的身高)求信号塔 的高度(结果保留根号).

如图所示,小明家与小华家住在同一栋楼的同一单元,他俩想测算所住楼对面商业大厦的高 .他俩在小明家的窗台 处,测得商业大厦顶部 的仰角 的度数,由于楼下植物的遮挡,不能在 处测得商业大厦底部 的俯角的度数.于是,他俩上楼来到小华家,在窗台 处测得大厦底部 的俯角 的度数,竟然发现 与 恰好相等.已知 , , 三点共线, , , , ,试求商业大厦的高 .

某市为了加快 网络信号覆盖,在市区附近小山顶架设信号发射塔,如图所示.小军为了知道发射塔的高度,从地面上的一点 测得发射塔顶端 点的仰角是 ,向前走60米到达 点测得 点的仰角是 ,测得发射塔底部 点的仰角是 .请你帮小军计算出信号发射塔 的高度.(结果精确到0.1米,

如图,校园内有两幢高度相同的教学楼 , ,大楼的底部 , 在同一平面上,两幢楼之间的距离 长为24米,小明在点 , , 在一条直线上)处测得教学楼 顶部的仰角为 ,然后沿 方向前进8米到达点 处,测得教学楼 顶部的仰角为 .已知小明的两个观测点 , 距离地面的高度均为1.6米,求教学楼 的高度 长.(精确到0.1米)参考值: , .

如图,为了测量山坡上一棵树 的高度,小明在点 处利用测角仪测得树顶 的仰角为 ,然后他沿着正对树 的方向前进 到达点 处,此时测得树顶 和树底 的仰角分别是 和 ,设 垂直于 ,且垂足为 .
(1)求 的度数;
(2)求树 的高度(结果精确到 , .

如图,为了测量建筑物 的高度,在 处竖立标杆 ,标杆的高是 ,在 上选取观测点 、 ,从 测得标杆和建筑物的顶部 、 的仰角分别为 、 .从 测得 、 的仰角分别为 、 .求建筑物 的高度(精确到 .(参考数据: , , .

如图,某高速公路建设中需要测量某条江的宽度 ,飞机上的测量人员在 处测得 , 两点的俯角分别为 和 .若飞机离地面的高度 为1200米,且点 , , 在同一水平直线上,则这条江的宽度 为 米(结果保留根号).

如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口 测得教学楼顶部 的仰角为 ,教学楼底部 的俯角为 ,量得实验楼与教学楼之间的距离 .
(1)求 的度数.
(2)求教学楼的高 .(结果精确到 ,参考数据: ,
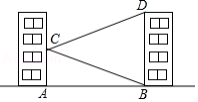
如图,在一次数学课外实践活动中,小聪在距离旗杆 的 处测得旗杆顶端 的仰角为 ,测角仪高 为 ,则旗杆高 为 (结果保留根号).

某游乐场一转角滑梯如图所示,滑梯立柱 、 均垂直于地面,点 在线段 上,在 点测得点 的仰角为 ,点 的俯角也为 ,测得 、 间距离为10米,立柱 高30米.求立柱 的高(结果保留根号)
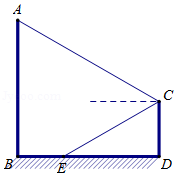
如图是某路灯在铅垂面内的示意图,灯柱 的高为11米,灯杆 与灯柱 的夹角 ,路灯采用锥形灯罩,在地面上的照射区域 长为18米,从 , 两处测得路灯 的仰角分别为 和 ,且 , ,求灯杆 的长度.

如图,甲建筑物 ,乙建筑物 的水平距离 为 ,且乙建筑物的高度是甲建筑物高度的6倍,从 , , 在同一水平线上)点测得 点的仰角为 ,测得 点的仰角为 ,求这两座建筑物顶端 、 间的距离(计算结果用根号表示,不取近似值).

无人机在 处测得正前方河流两岸 、 的俯角分别为 、 ,此时无人机的高度是 ,则河流的宽度 为

A. B.
C. D.