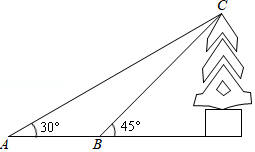
在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度.用测角仪在 处测得雕塑顶端点 的仰角为 ,再往雕塑方向前进4米至 处,测得仰角为 .问:该雕塑有多高?(测角仪高度忽略不计,结果不取近似值.
相关知识点
推荐套卷
在数学实践活动课上,老师带领同学们到附近的湿地公园测量园内雕塑的高度.用测角仪在 处测得雕塑顶端点 的仰角为 ,再往雕塑方向前进4米至 处,测得仰角为 .问:该雕塑有多高?(测角仪高度忽略不计,结果不取近似值.
