如,已知抛物线y = ax2+bx+ c经过坐标原点,与x轴的另一个交点为A,且顶点M坐标为(1,2),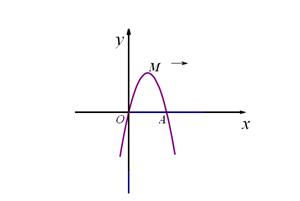
(1)求该抛物线的解析式;
(2)现将它向右平移m(m>0)个单位,所得抛物线与x轴交于C、D两点,与原抛物线交于点P,△CDP的面积为S,求S关于m的关系式;
(3)如图,以点A为圆心,以线段OA为半径画圆交抛物线y = ax2+bx+ c的对称轴于点B,连结AB,
若将抛物线向右平移m(m>0)个单位后,B点的对应点为B′,A点的对应点为A′点,且满足四边形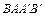 为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
为菱形,平移后的抛物线的对称轴与菱形的对角线BA′交于点E,在x轴上是否存在一点F,
使得以E、F、A′为顶点的三角形与△BAE相似,若存在求出F点坐标,若不存在说明理由. 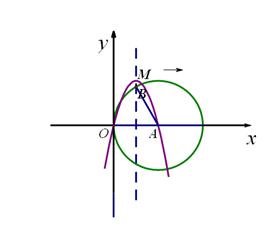
相关知识点
推荐套卷



 粤公网安备 44130202000953号
粤公网安备 44130202000953号