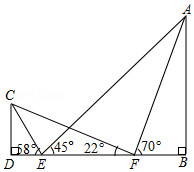
如图,为了测量建筑物 的高度,在 处竖立标杆 ,标杆的高是 ,在 上选取观测点 、 ,从 测得标杆和建筑物的顶部 、 的仰角分别为 、 .从 测得 、 的仰角分别为 、 .求建筑物 的高度(精确到 .(参考数据: , , .
相关知识点
推荐套卷
如图,为了测量建筑物 的高度,在 处竖立标杆 ,标杆的高是 ,在 上选取观测点 、 ,从 测得标杆和建筑物的顶部 、 的仰角分别为 、 .从 测得 、 的仰角分别为 、 .求建筑物 的高度(精确到 .(参考数据: , , .
