如图所示，学校操场上有一旗杆AB，甲在操场上的C处直立一根3米高的竹竿CD，甲从C处退后3米到达E处，恰好看到竹竿的顶端D与旗杆的顶端B重合，甲的眼睛到地面的距离FE为1.5米，身高相同的乙在C1处也直立一根3米高的竹竿C1D1，乙从C1处退后4米到达E1处，恰好看到竹竿的顶端D1与旗杆的顶端B也重合(点A，C，E，C1，E1在同一条直线上)，量得EE1＝6米，求旗杆AB的高．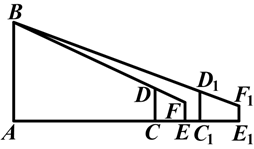
如图所示，学校操场上有一旗杆AB，甲在操场上的C处直立一根3米高的竹竿CD，甲从C处退后3米到达E处，恰好看到竹竿的顶端D与旗杆的顶端B重合，甲的眼睛到地面的距离FE为1.5米，身高相同的乙在C1处也直立一根3米高的竹竿C1D1，乙从C1处退后4米到达E1处，恰好看到竹竿的顶端D1与旗杆的顶端B也重合(点A，C，E，C1，E1在同一条直线上)，量得EE1＝6米，求旗杆AB的高．
粤公网安备 44130202000953号