初中数学解直角三角形的应用-仰角俯角问题试题

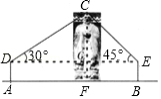
在一次课外活动中，甲、乙两位同学测量公园中孔子塑像的高度，他们分别在 $A$， $B$两处用高度为 $1.5m$的测角仪测得塑像顶部 $C$的仰角分别为 $30°$， $45°$，两人间的水平距离 $\mathit{AB}$为 $10m$，求塑像的高度 $\mathit{CF}$．（结果保留根号）

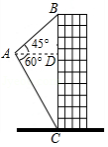
如图，光明中学一教学楼顶上竖有一块高为 $\mathit{AB}$的宣传牌，点 $E$和点 $D$分别是教学楼底部和外墙上的一点 $(A$， $B$， $D$， $E$在同一直线上），小红同学在距 $E$点9米的 $C$处测得宣传牌底部点 $B$的仰角为 $67°$，同时测得教学楼外墙外点 $D$的仰角为 $30°$，从点 $C$沿坡度为 $1:\sqrt{3}$的斜坡向上走到点 $F$时， $\mathit{DF}$正好与水平线 $\mathit{CE}$平行．

（1）求点 $F$到直线 $\mathit{CE}$的距离（结果保留根号）；

（2）若在点 $F$处测得宣传牌顶部 $A$的仰角为 $45°$，求出宣传牌 $\mathit{AB}$的高度（结果精确到 $0.01)$．（注 $:\sin 67°\approx 0.92$， $\tan 67°\approx 2.36$， $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$

关于三角函数有如下公式： $\sin (\alpha +\beta )=\sin \alpha \cos \beta +\cos \alpha \sin \beta$， $\sin (\alpha -\beta )=\sin \alpha \cos \beta -\cos \alpha \sin \beta$

$\cos (\alpha +\beta )=\cos \alpha \cos \beta -\sin \alpha \sin \beta$， $\cos (\alpha -\beta )=\cos \alpha \cos \beta +\sin \alpha \sin \beta$

$\tan (\alpha +\beta )=\frac{\tan \alpha +\tan \beta }{1-\tan \alpha \tan \beta }(1-\tan \alpha \tan \beta \ne 0)$

$\tan (\alpha -\beta )=\frac{\tan \alpha -\tan \beta }{1+\tan \alpha \tan \beta }(1+\tan \alpha \tan \beta \ne 0)$

利用这些公式可以将一些不是特殊角的三角函数转化为特殊角的三角函数来求值．

如： $\tan 105°=\tan (45°+60°)=\frac{\tan 45°+\tan 60°}{1-\tan 45°\tan 60°}=\frac{1+\sqrt{3}}{1-\sqrt{3}}=-2-\sqrt{3}$

根据上面的知识，你可以选择适当的公式解决下面问题：

如图，两座建筑物 $\mathit{AB}$和 $\mathit{DC}$的水平距离 $\mathit{BC}$为24米，从点 $A$测得点 $D$的俯角 $\alpha =15°$，测得点 $C$的俯角 $\beta =75°$，求建筑物 $\mathit{CD}$的高度．

如图，某人为了测量小山顶上的塔的高，他在山下的点处测得塔尖点的仰角为，再沿方向前进到达山脚点，测得塔尖点的仰角为，塔底点的仰角为，求塔的高度．（结果保留根号）

如图，为了测得一棵树的高度 $\mathit{AB}$，小明在 $D$处用高为 $1m$的测角仪 $\mathit{CD}$，测得树顶 $A$的仰角为 $45°$，再向树方向前进 $10m$，又测得树顶 $A$的仰角为 $60°$，求这棵树的高度 $\mathit{AB}$．

如图，航拍无人机从 $A$处测得一幢建筑物顶部 $B$的仰角为 $45°$，测得底部 $C$的俯角为 $60°$，此时航拍无人机与该建筑物的水平距离 $\mathit{AD}$为 $110m$，那么该建筑物的高度 $\mathit{BC}$约为　        $m$（结果保留整数， $\sqrt{3}\approx 1.73)$．

荆州市滨江公园旁的万寿宝塔始建于明嘉靖年间，周边风景秀丽．现在塔底低于地面约7米，某校学生测得古塔的整体高度约为40米．其测量塔顶相对地面高度的过程如下：先在地面 $A$处测得塔顶的仰角为 $30°$，再向古塔方向行进 $a$米后到达 $B$处，在 $B$处测得塔顶的仰角为 $45°$（如图所示），那么 $a$的值约为　    　米 $(\sqrt{3}\approx 1.73$，结果精确到 $0.1)$．

如图，在水平地面上有一幢房屋 $\mathit{BC}$与一棵树 $\mathit{DE}$，在地面观测点 $A$处测得屋顶 $C$与树梢 $D$的仰角分别是 $45°$与 $60°$， $\angle \mathit{CAD}=60°$，在屋顶 $C$处测得 $\angle \mathit{DCA}=90°$．若房屋的高 $\mathit{BC}=6$米，求树高 $\mathit{DE}$的长度．

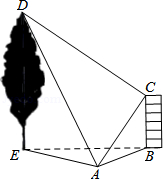
数学实践活动小组借助载有测角仪的无人机测量象山岚光阁与文明湖湖心亭之间的距离．如图，无人机所在位置 $P$与岚光阁阁顶 $A$、湖心亭 $B$在同一铅垂面内， $P$与 $B$的垂直距离为300米， $A$与 $B$的垂直距离为150米，在 $P$处测得 $A$、 $B$两点的俯角分别为 $\alpha$、 $\beta$，且 $\tan \alpha =\frac{1}{2}$， $\tan \beta =\sqrt{2}-1$，试求岚光阁与湖心亭之间的距离 $\mathit{AB}$．（计算结果若含有根号，请保留根号）

如图，无人机在空中 $C$处测得地面 $A$、 $B$两点的俯角分别为 $60°$、 $45°$，如果无人机距地面高度 $\mathit{CD}$为 $100\sqrt{3}$米，点 $A$、 $D$、 $B$在同一水平直线上，则 $A$、 $B$两点间的距离是　                      　米．（结果保留根号）

如图，在大楼 $\mathit{AB}$正前方有一斜坡 $\mathit{CD}$，坡角 $\angle \mathit{DCE}=30°$，楼高 $\mathit{AB}=60$米，在斜坡下的点 $C$处测得楼顶 $B$的仰角为 $60°$，在斜坡上的 $D$处测得楼顶 $B$的仰角为 $45°$，其中点 $A$， $C$， $E$在同一直线上．

（1）求坡底 $C$点到大楼距离 $\mathit{AC}$的值；

（2）求斜坡 $\mathit{CD}$的长度．

如图， $\mathit{AB}$和 $\mathit{CD}$两幢楼地面距离 $\mathit{BC}$为 $30\sqrt{3}$米，楼 $\mathit{AB}$高30米，从楼 $\mathit{AB}$的顶部点 $A$测得楼 $\mathit{CD}$的顶部点 $D$的仰角为 $45°$．

（1）求 $\angle \mathit{CAD}$的大小；

（2）求楼 $\mathit{CD}$的高度（结果保留根号）．

风电已成为我国继煤电、水电之后的第三大电源，风电机组主要由塔杆和叶片组成（如图1），图2是从图1引出的平面图．假设你站在 $A$处测得塔杆顶端 $C$的仰角是 $55°$，沿 $\mathit{HA}$方向水平前进43米到达山底 $G$处，在山顶 $B$处发现正好一叶片到达最高位置，此时测得叶片的顶端 $D(D$、 $C$、 $H$在同一直线上）的仰角是 $45°$．已知叶片的长度为35米（塔杆与叶片连接处的长度忽略不计），山高 $\mathit{BG}$为10米， $\mathit{BG}\perp \mathit{HG}$， $\mathit{CH}\perp \mathit{AH}$，求塔杆 $\mathit{CH}$的高．（参考数据： $\tan 55°\approx 1.4$， $\tan 35°\approx 0.7$， $\sin 55°\approx 0.8$， $\sin 35°\approx 0.6)$

在数学实践与综合课上，某兴趣小组同学用航拍无人机对某居民小区的1、2号楼进行测高实践，如图为实践时绘制的截面图．无人机从地面点 $B$垂直起飞到达点 $A$处，测得1号楼顶部 $E$的俯角为 $67°$，测得2号楼顶部 $F$的俯角为 $40°$，此时航拍无人机的高度为60米，已知1号楼的高度为20米，且 $\mathit{EC}$和 $\mathit{FD}$分别垂直地面于点 $C$和 $D$，点 $B$为 $\mathit{CD}$的中点，求2号楼的高度．（结果精确到 $0.1)$

（参考数据 $\sin 40°\approx 0.64$， $\cos 40°\approx 0.77$， $\tan 40°\approx 0.84$， $\sin 67°\approx 0.92$， $\cos 67°\approx 0.39$， $\tan 67°\approx 2.36)$

金桥学校“科技体艺节”期间，八年级数学活动小组的任务是测量学校旗杆 $\mathit{AB}$的高，他们在旗杆正前方台阶上的点 $C$处，测得旗杆顶端 $A$的仰角为 $45°$，朝着旗杆的方向走到台阶下的点 $F$处，测得旗杆顶端 $A$的仰角为 $60°$，已知升旗台的高度 $\mathit{BE}$为1米，点 $C$距地面的高度 $\mathit{CD}$为3米，台阶 $\mathit{CF}$的坡角为 $30°$，且点 $E$、 $F$、 $D$在同一条直线上，求旗杆 $\mathit{AB}$的高度（计算结果精确到0.1米，参考数据： $\sqrt{2}\approx 1.41$， $\sqrt{3}\approx 1.73)$