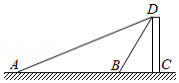
如图,为测量建筑物 的高度,在 点测得建筑物顶部 点的仰角为 ,再向建筑物 前进30米到达 点,测得建筑物顶部 点的仰角为 , , 三点在一条直线上),求建筑物 的高度.(结果保留整数.参考数据: , , , , ,
相关知识点
推荐套卷
如图,为测量建筑物 的高度,在 点测得建筑物顶部 点的仰角为 ,再向建筑物 前进30米到达 点,测得建筑物顶部 点的仰角为 , , 三点在一条直线上),求建筑物 的高度.(结果保留整数.参考数据: , , , , ,
