如图,在 中,半径 ,过点 的中点 作 交 于 、 两点,且 ,以 为圆心, 为半径作 ,交 于 点.
(1)求 的半径 的长;
(2)计算阴影部分的面积.

(本小题满分8分)马航MH370失联后,我国政府积极参与搜救.某日,我国两艘专业救助船A、B同时收到有关可疑漂浮物的讯息,可疑漂浮物P在救助船A的北偏东53.50°方向上,在救助船B的西北方向上,船B在船A正东方向140海里处.(参考数据:sin36.5°≈0.6,cos36.5°≈0.8,tan36.5°≈0.75).
(1)求可疑漂浮物P到A、B两船所在直线的距离;
(2)若救助船A、救助船B分别以40海里/时,30海里/时的速度同时出发,匀速直线前往搜救,试通过计算判断哪艘船先到达P处.
如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的 交AC于点E,F是
交AC于点E,F是 上的点,且AF=BF.
上的点,且AF=BF.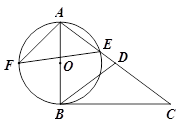
(1)求证:BC是 的切线;
的切线;
(2)若sinC=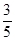 ,AE=
,AE=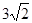 ,求sinF的值和AF的长.
,求sinF的值和AF的长.
已知四边形 的一组对边 、 的延长线交于点 .
(1)如图1,若 ,求证: ;
(2)如图2,若 , , , , 的面积为6,求四边形 的面积;
(3)如图3,另一组对边 、 的延长线相交于点 .若 , , ,直接写出 的长(用含 的式子表示)

如图,在△ABC中,∠ABC=90°,以AB的中点O为圆心,OA为半径的圆交AC于点D,E是BC的中点,连接DE,OE.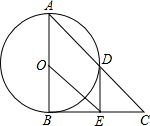
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若cos∠BAD= ,BE=
,BE= ,求OE的长.
,求OE的长.
如图,把 放置在菱形 中,使得顶点 , , 分别在线段 , , 上,已知 , , ,且 .
(1)求 的大小;
(2)若 ,求 的值;
(3)若 的三个顶点 、 、 分别在线段 、 、 上运动,请直接写出 长的最大值和最小值.

问题:已知 、 均为锐角, , ,求 的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
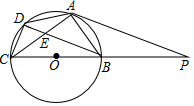
如图,已知 是 的直径, 为 上(异于 、 一点, 的切线 与 的延长线交于点 ; 为 上一点, 的延长线交 于点 , 为 上一点且 , 的延长线交 于点 .
(1)求证: ;
(2)若 、 的长是一元二次方程 的两根,求 的长;
(3)若 , ,求 的长.
如图1, 的边 在 轴的正半轴上, ,反比例函数 的图象经过点 .
(1)求反比例函数的关系式和点 的坐标;
(2)如图2,过 的中点 作 轴交反比例函数图象于点 ,连接 、 .
①求 的面积;
②在 的边上是否存在点 ,使得 是以 为斜边的直角三角形?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
