江苏省扬州市直学校九年级第二次模拟考试数学试卷
2015年,扬州中考考生约36000人,则数据36000用科学记数法表示为( )
| A.0.36×105 | B.3.6×103 | C.3.6×104 | D.3.6×105 |
如图,直线a∥b,点C在直线 上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
上,∠DCB=90°,若∠1=70°,则∠2的度数为( )
| A.20° | B.25° | C.30° | D.40° |
为了解某小区“全民健身”活动的开展情况,某志愿者对居住在该小区的50名成年人一周的体育锻炼时间进行了统计,并绘制成如图所示的条形统计图.这组数据的众数和中位数分别是( )
| A.6,4 | B.6,6 | C.4,4 | D.4,6 |
我们常用“y随x的增大而增大(或减小)”来表示两个变量之间的变化关系.有这样一个情境:如图,小王从点A经过路灯C的正下方沿直线走到点B,他与路灯C的距离y随他与点A之间的距离x的变化而变化.下列函数中y与x之间的变化关系,最有可能与上述情境类似的是( )
A.y= |
B.y=-x+3 | C.y=-(x-3)2+3 | D.y=(x-3)2+3 |
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A' 恰好落在∠BCD的平分线上时,C A' 的长为( )
A.3或4 |
B.3 或4 或4 |
C.3或4 | D.4或3 |
某学习小组设计了一个摸球试验,在袋中装有黑,白两种颜色的球,这些球的形状大小质地等完全相同,即除颜色外无其他差别.在看不到球的情况下,随机从袋中摸出一个球,记下颜色,再把它放回,不断重复.下表是由试验得到的一组统计数据:
| 摸球的次数n |
100 |
200 |
300 |
400 |
500 |
600 |
| 摸到白球的次数m |
58 |
118 |
189 |
237 |
302 |
359 |
摸到白球的频率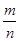 |
0.58 |
0.59 |
0.63 |
0.593 |
0.604 |
0.598 |
从这个袋中随机摸出一个球,是白球的概率约为 .(结果精确到0.1)
如图,跷跷板AB的支柱OD经过它的中点O,且垂直于地面BC,垂足为D,OD=
45cm,当它的一端B着地时,另一端A离地面的高度AC为 cm.
已知Rt△ABC,∠C=90°,AB=13,AC=12,以AC所在直线为轴将此三角形旋转一周所得圆锥的侧面积是 .(结果保留 )
)
在□ABCD中,AB=3,BC=4,当□ABCD的面积最大时,下列结论:
①AC=5;②∠A+∠C=180°;③AC⊥BD;④AC=BD.
其中正确的有 °.(填序号)
在一次数学游戏中,老师在 三个盘子里分别放了一些糖果,糖果数依次为
三个盘子里分别放了一些糖果,糖果数依次为 ,
, ,
, ,记为
,记为 (
( ,
, ,
, ).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束.
).游戏规则如下:若三个盘子中的糖果数不完全相同,则从糖果数最多的一个盘子中拿出两个,给另外两个盘子各放一个(若有两个盘子中的糖果数相同,且都多于第三个盘子中的糖果数,则从这两个盘子字母序在前的盘子中取糖果),记为一次操作.若三个盘子中的糖果数都相同,游戏结束. 次操作后的糖果数记为
次操作后的糖果数记为 (
( ,
, ,
, ).小明发现:若
).小明发现:若 (4,8,18),则游戏永远无法结束,那么
(4,8,18),则游戏永远无法结束,那么 .
.
小晗家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下其中的两个开关,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表加以说明.
“低碳环保,你我同行”.两年来,扬州市区的公共自行车给市民出行带来切实方便.电视台记者在某区街头随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况:
| A.每天都用; | B.经常使用; | C.偶尔使用; | D.从未使用.将这次调查情况整理并绘制如下两幅统计图: |

根据图中的信息,解答下列问题:
(1)本次活动共有 位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若该区有46万市民,请估算每天都用公共自行车的市民约有多少人?
已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形 AMCN是菱形,证明你的结论.
学校举行数学知识竞赛,设立了一、二、三等奖,计划共购买45件奖品,其中二等奖奖品件数比一等奖奖品件数的2倍还少5件,已知购买一等奖奖品x件.各种奖品的单价如下表.
| 奖品 |
一等奖奖品 |
二等奖奖品 |
三等奖奖品 |
| 单价(元) |
12 |
10 |
8 |
(1)学校购买二等奖奖品 件,三等奖奖品 件;(用含x的代数式表示)
(2)若购买三等奖奖品的费用不超过二等奖奖品费用的2倍,学校为节省开支,应如何购买这三种奖品?总费用最少是多少元?
如图,“和谐号”高铁列车的小桌板收起时,小桌板的支架底端与桌面顶端的距离OA=75厘米,且可以近似看作与地面垂直.展开小桌板使桌面保持水平,此时CB⊥AO,∠AOB=∠ACB=37°,且支架长OB与桌面宽BC的长度之和等于OA的长度.求小桌板桌面的宽度BC.(参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
如图,在△ABC中,点D在AC上,DA=DB,∠C=∠DBC,以AB为直径的 交AC于点E,F是
交AC于点E,F是 上的点,且AF=BF.
上的点,且AF=BF.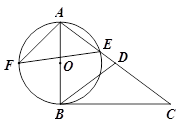
(1)求证:BC是 的切线;
的切线;
(2)若sinC=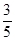 ,AE=
,AE=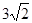 ,求sinF的值和AF的长.
,求sinF的值和AF的长.
在平面直角坐标系xOy中,抛物线 经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
经过点N(2,-5),过点N作x轴的平行线交此抛物线左侧于点M,MN=6.
(1)求此抛物线的解析式;
(2)点P(x,y)为此抛物线上一动点,连接MP交此抛物线的对称轴于点D,当△DMN为直角三角形时,求点P的坐标;
(3)设此抛物线与y轴交于点C,在此抛物线上是否存在点Q,使∠QMN=∠CNM ?若存在,求出点Q的坐标;若不存在,说明理由.


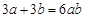
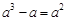
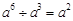
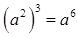





 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . 的图象与直线
的图象与直线 没有交点,则k的取值范围是 .
没有交点,则k的取值范围是 . 有两个相等的实数根,则
有两个相等的实数根,则 .
. 上,则∠E= °.
上,则∠E= °.
 ;
; .
. ,其中
,其中 是不等式组
是不等式组 的一个整数解.
的一个整数解.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号