如图,已知 ,垂足为 , , ,将线段 绕点 按逆时针方向旋转 ,得到线段 ,连接 , .
(1)线段 ;
(2)求线段 的长度.

一次函数 的图象与 轴的负半轴相交于点 ,与 轴的正半轴相交于点 ,且 . 的外接圆的圆心 的横坐标为 .
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.

如图,在四边形 中, , , ,以点 为圆心, 为半径的圆与 相切于点 ,交 于点
(1)求 的大小及 的长度;
(2)在 的延长线上取一点 ,使得 上的一个动点 到点 的最短距离为 ,求 的长.

如图, 为 的直径, 为 上一点,经过点 的切线交 的延长线于点 , 交 的延长线于点 , 交 于 , 于 ,分别交 、 于 、 ,连接 , .
(1)求证: 平分 ;
(2)若 , ,
①求 的半径;
②求 的长.

如图,在 中,半径 ,过点 的中点 作 交 于 、 两点,且 ,以 为圆心, 为半径作 ,交 于 点.
(1)求 的半径 的长;
(2)计算阴影部分的面积.

已知四边形 的一组对边 、 的延长线交于点 .
(1)如图1,若 ,求证: ;
(2)如图2,若 , , , , 的面积为6,求四边形 的面积;
(3)如图3,另一组对边 、 的延长线相交于点 .若 , , ,直接写出 的长(用含 的式子表示)

如图,把 放置在菱形 中,使得顶点 , , 分别在线段 , , 上,已知 , , ,且 .
(1)求 的大小;
(2)若 ,求 的值;
(3)若 的三个顶点 、 、 分别在线段 、 、 上运动,请直接写出 长的最大值和最小值.

问题:已知 、 均为锐角, , ,求 的度数.
探究:(1)用6个小正方形构造如图所示的网格图(每个小正方形的边长均为 ,请借助这个网格图求出 的度数;
延伸:(2)设经过图中 、 、 三点的圆弧与 交于 ,求 的弧长.

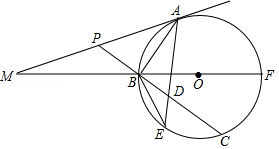
如图,四边形 内接于 , 为 的直径, 与 交于点 , 为 延长线上一点,连接 ,且 .
(1)求证: 为 的切线;
(2)若 , ,求 长;
(3)在(2)的条件下,若 ,求 的面积.
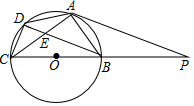
如图,已知 是 的直径, 为 上(异于 、 一点, 的切线 与 的延长线交于点 ; 为 上一点, 的延长线交 于点 , 为 上一点且 , 的延长线交 于点 .
(1)求证: ;
(2)若 、 的长是一元二次方程 的两根,求 的长;
(3)若 , ,求 的长.
如图1, 的边 在 轴的正半轴上, ,反比例函数 的图象经过点 .
(1)求反比例函数的关系式和点 的坐标;
(2)如图2,过 的中点 作 轴交反比例函数图象于点 ,连接 、 .
①求 的面积;
②在 的边上是否存在点 ,使得 是以 为斜边的直角三角形?若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
